Hint for Section 1.3 Question 1c: Truth table approach
1c) Let c represent "the cat fiddled", let j
represent "the cow jumped over the moon", let d represent "the
little dog laughed", and let r represent "the dish ran away with the
spoon." Now write each of the premises and the conclusion in symbolic form.
The first premise (p1) is "If the cat fiddled or the cow
jumped over the moon, then the little dog laughed." This can be written symbolically
as (c V j) 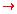 d.
d.
The second premise (p2) is "If the little dog laughed, then the dish ran
away with the spoon." This can be written symbolically as d
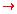 r.
r.
The third premise (p3) is "But the dish did not run away with the
spoon." This can be written symbolically as ~r.
The conclusion (q) is "Therefore the cat did not fiddle." This can be written
symbolically as ~c.
Remember that an argument is written as a conjunction of the premises
implies the conclusion. So this argument can be represented as
[(c V j) 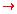 d) L (d
d) L (d 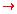 r)
L (~r)]
r)
L (~r)] 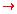 (~c).
(~c).
Now construct a truth table.
| c |
j |
d |
r |
|
(c V j)
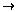 d d |
d 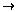 r r |
~r |
|
~c |
| T |
T |
T |
T |
|
T |
T |
F |
|
F |
| T |
T |
T |
F |
|
T |
F |
T |
|
F |
| T |
T |
F |
T |
|
F |
T |
F |
|
F |
| T |
T |
F |
F |
|
F |
T |
T |
|
F |
| T |
F |
T |
T |
|
T |
T |
F |
|
F |
| T |
F |
T |
F |
|
T |
F |
T |
|
F |
| T |
F |
F |
T |
|
F |
T |
F |
|
F |
| T |
F |
F |
F |
|
F |
T |
T |
|
F |
| F |
T |
T |
T |
|
T |
T |
F |
|
T |
| F |
T |
T |
F |
|
T |
F |
T |
|
T |
| F |
T |
F |
T |
|
F |
T |
F |
|
T |
| F |
T |
F |
F |
|
F |
T |
T |
|
T |
| F |
F |
T |
T |
|
T |
T |
F |
|
T |
| F |
F |
T |
F |
|
T |
F |
T |
|
T |
| F |
F |
F |
T |
|
T |
T |
F |
|
T |
| F |
F |
F |
F |
|
T |
T |
T |
|
T |
The critical rows of the truth table are the rows in which all the premises are true.
Identify these rows. Recall that an argument is valid if the conclusion is true in all the
critical rows.
Back to Section 1.3
Full solution