Chapter Eleven
Graph Theory
Section 11.1
An Introduction
The following solutions make use of information found on pages 602 - 616 of the
textbook.
Exercise 11.1.1: Definitions
Fill in the blanks to complete the following sentences.
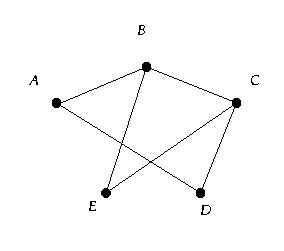
- Imagine a medical practitioner working out of six different
surgeries. At each surgery there is a computer used to store medical
records. To allow patients to freely visit any one of the surgeries,
the six different computers are to be networked. Analysis shows that
the following connections are optimal:
- connect computer A with computers B and D;
- connect computer B with computers A, C and E;
- connect computer C with computers B, D and E;
- connect computer D with computers A and C;
- connect computer E with computers B and C;
In the following diagram, the dots represent the computers. Illustrate the computer
connections by drawing straight lines to represent each connection.
A network can be represented by a graph.
The dots (or nodes in the network) are called
vertices (plural of
vertex)
and the line segments joining vertices are called
edges.
- A graph G consists of two finite sets:
- a set V(G) of vertices, and
- a set E(G) of edges,
where each edge is associated with a set consisting of either
one or two vertices called
its endpoints.
It is assumed that
V(G)  Æ. That is, the
vertex set V(G)
is assumed to be non-empty.
Æ. That is, the
vertex set V(G)
is assumed to be non-empty.
A loop is an edge with just one
endpoint.
Parallel edges are two or more distinct edges with the
same set of endpoints.
An edge is said to be incident on each of its
endpoints.
Two edges are adjacent if they are incident on the same
vertex.
Two vertices are said to be adjacent if they are connected by
an edge.
A vertex that is an endpoint of a
loop is said to be adjacent to itself.
An isolated vertex is a vertex which is incident on
no edges.
- Let G be a graph.
( i ) The edge set, E(G), consists of subsets of V(G) of size 1 or
2.
( ii ) The vertices x,y Î V(G) are adjacent
if, and only if, {x,y}Î E(G).
( iii ) The edges {x,y}, {u,v} Î E(G) are adjacent if, and
only if, one of the following statements is true: x = u, x = v, y =
u or y = v.
( iv ) List the edge set for the graph you drew for the computer connections. {{A,B},{A,D},{B,E},{B,C},{C,E,},{C,D}}.
- A directed graph, or digraph, consists of
two finite sets:
- a set V(G) of vertices, and
- a set E(G) of directed
edges, where each edge is associated with an ordered pair of
vertices called its endpoints.
If e is an edge in a directed graph and e is associated with the
ordered pair (v,w) of vertices,
then e is said to be the (directed) edge
from v to w.
- A simple graph has no loops
or parallel edges.
- A complete graph, denoted Kn, on n vertices,
v1, v2, ..., vn, is a simple graph with
an edge connecting every
pair of distinct
vertices.
- A bipartite graph is a simple graph whose vertex set can be partitioned into two
disjoint sets V1 = {v1,v2, ..., vm} and V2
= {w1, w2, ..., wn} such that every edge of the graph has
one endpoint in the set V1 and the other endpoint in the set V2.
Use
the above definition to complete the following statement.
A complete bipartite graph on m + n vertices, denoted Km,n, is a
bipartite graph with vertices V1 = {v1,v2,...,vm}
and V2 = {w1,w2,...,wn} in which every vertex
in V1 is adjacent to every vertex in V2,
no pair of vertices from V1 are adjacent, and no pair of
vertices in V2 are adjacent.
- A graph H is said to be a subgraph of a graph G if, and only if, every vertex in
H is also a vertex in G, every edge in H is also an edge in G, and every edge in H has the same endpoints as in G.
- Let G be a graph and v a vertex of G. The degree of v, denoted deg(v),
equals the number of edges that are incident on v, with an edge that
is a loop counted twice. The total degree of G is the
sum of the degrees of all the vertices of G.
- Theorem If G is any graph, then the sum of the degrees
of all the vertices of G equals twice the number of edges of G.
Equivalently, for any graph G with vertex set
V(G)={v1,v2,¼,
vn}, then
| the total degree of G |
= |
deg(v1) + deg(v2) + ... + deg(vn)
|
|
= |
2(the number of edges of G) |
|
= |
2 |E(G)|. |
- Corollary The total degree of a graph is even.
- Lemma In any graph there is an even number of
vertices of odd degree.
Exercise 11.1.2: Examples
You should attempt all these exercises yourself, using the textbook as an aid. Once you
have attempted each question, check your answers by following the appropriate links. If
you are stuck on a question, choose the link that gives you a hint and then try the
question again.
1. In the following graph determine the sets of: vertices, edges, loops, isolated vertices
and parallel edges.
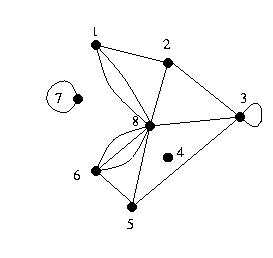
Full solution
2. Consider the graph specified as follows:
| vertex set |
= |
{v1,v2,v3,v4,v5,v6},
|
| edge set |
= |
{{v1,v2},{v2,v3},{v3,v4},{v4,v5}, |
|
|
{v3,v5},{v1,v3}, {v6,v6},{v3,v6}}.
|
Draw this graph.
Full solution
3. List the vertex set and edge set for each of these two graphs and verify that they
are two representations of the same graph.
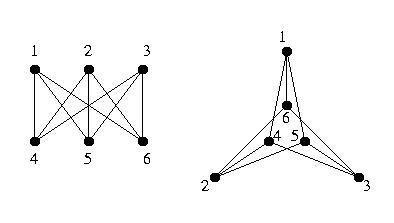
Full solution
4. For each of the following graphs, determine whether or not the graph is bipartite.
Explain your answers.
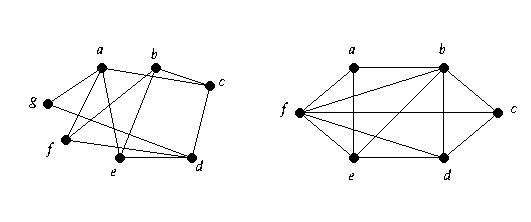
Hint
Full solution
5. Find all nonempty subgraphs of the following graph.
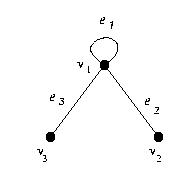
Hint
Full solution
6. Show that the complete graph on seven vertices is a subgraph of the complete graph
on ten vertices.
Hint
Full solution
7. Find the total degree of the graph in Question 1. Then apply Theorem 11.1.1 to
calculate the number of edges in the graph.
Hint
Full solution
8. Is there a graph with seven vertices of degrees 2, 3, 3, 4, 4, 5 and 6?
Explain your answer.
Hint
Full solution
9. Either draw a graph with ten vertices in which each vertex has degree 3, or show
that such a graph cannot exist.
Full solution
10. Königsberg bridge problem. The town of Königsberg in Prussia was
built at a point where two branches of the Pregel River met. The town encompassed an
island and land adjacent to the river banks. These were connected by seven bridges as
shown in the following figure.
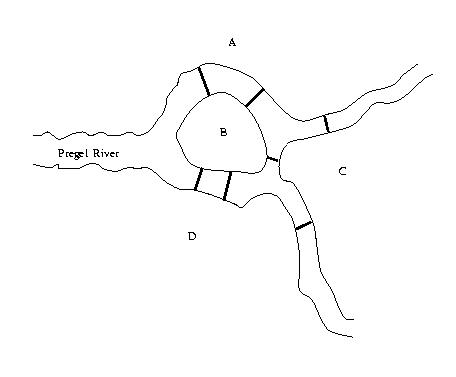
Draw a graph which represents the river crossings of Königsberg.
Hint
Full solution
Section 11.2
Paths and Circuits
The following solutions make use of information found on pages 619 - 635 of the
textbook.
Exercise 11.2.1: Definitions
Fill in the blanks to complete the following sentences.
- Let G be a graph and let v and w be vertices in G.
A walk from v to w is a finite
alternating sequence of adjacent vertices and edges of G.
A walk has the form v0e1v1e2...
vn-1envn, where the v's
represent vertices, and the e's represent edges.
The trivial walk from v to v consists of
a single vertex. Hence a trivial walk
contains no edges and so a loop is
not a trivial walk.
- Given a walk v0e1v1e2
...vn-1envn if there is no
ambiguity, then the notation is sometimes simplified to
v0v1v2 ... vn or
to e1e2 ... en.
- A path from v to w is a walk from
v to w that does not contain a repeated edge.
In a simple path from v to w there are
no
repeated vertices.
- A closed walk is a walk that starts
and ends at the same
vertex.
- A circuit is a closed walk
that does not contain a repeated
edge.
A simple circuit is a circuit in which the only repeated
vertices are the first
and the last.
- Let G be a graph. Two vertices v and w of G are connected
if, and only if, there is a walk from v to w.
The graph G is connected if,
and only if, given any two vertices v and w in G
there is a
walk from v to w.
Symbolically: G is connected Û " v,w Î V(G), $
a walk from v to w.
- Lemma Let G be a graph.
- If G is connected, then any two distinct vertices of G
are
connected by a simple path.
- If G contains a circuit incident with vertices v and w,
and one edge is removed from the circuit,
then there still exists a path from
v to w in G.
- If G is connected and G contains a circuit, then
an edge of the
circuit can be removed without disconnecting G.
- Let G be a graph. An Euler circuit for G is a circuit that
is incident with
every vertex of G and uses every edge of G
exactly once.
- Theorem A nonempty graph G has an Euler circuit if,
and only if, G is connected and every
vertex of G has even
degree.
- Thus if a nonempty graph G contains a vertex of
odd degree, then the graph does not
have an Euler circuit.
- Let G be a graph and let v and w be two vertices of G.
An Euler path from v to w
is a path that starts at the vertex v,
ends at the vertex w, passes through every vertex of G at least once,
and traverses every edge of G
exactly once.
- Corollary Let G be a graph and let v and w be
two vertices of G. There is
an Euler path from v to w if, and only if,
G is connected, v and w
have odd degree, and all other vertices have even degree.
Exercise 11.2.2: Examples
You should attempt all these exercises yourself, using the textbook as an aid. Once you
have attempted each question, check your answers by following the appropriate links. If
you are stuck on a question, choose the link that gives you a hint and then try the
question again.
1. Consider the following graph.
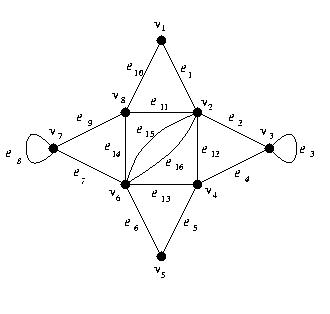
Determine which of the following walks are paths, simple paths, circuits, and/or simple
circuits.
a) v3v4v6v8v1v2v3.
b) e1e11e14e7e8e9e10.
c) v1e1v2e11v8e14v6e15v2e1v1.
d) v1e1v2e2v3e4v4e5v5e6v6e7v7e9v8.
Hint
Full solution
2. Consider the following map showing several cities and the roads connecting them. Is
it possible for a travelling salesman to find a route which passes through each of the
cities exactly once (not necessarily using all the roads) and end up where he started? Is
it possible for the travelling salesman to pass through the cities using all of the roads
exactly once? Explain your answers.
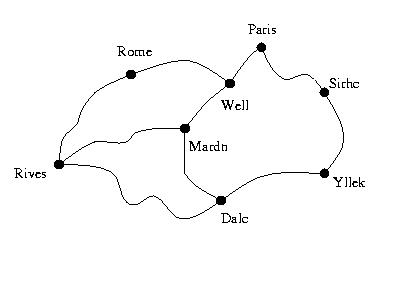
Hint
Full solution
3. Königsberg bridge problem. Consider Section 11.1, Question 10.
Is it possible to take a walk around Königsberg in such a way as to cross each of
the seven bridges exactly once? Explain your answer.
Hint
Full solution
4. Determine whether each of the following graphs has an Euler circuit. For each
graph that does have an Euler circuit, write out the circuit. For each graph which does
not have an Euler circuit, determine whether the graph has an Euler path, and if it does,
write out the Euler path.
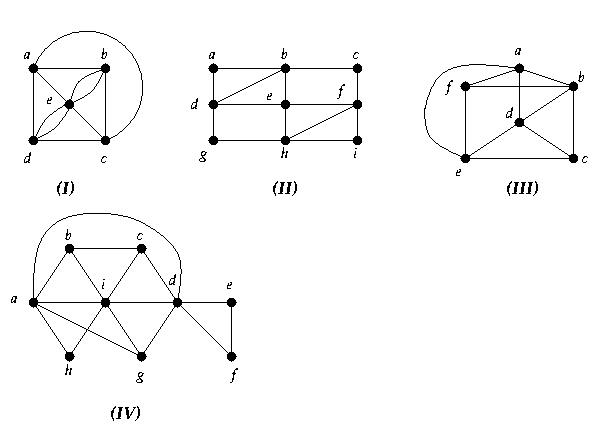
Hint
Full solution
Section 11.3
Matrix Representations of Graphs
The following solutions make use of information found on pages 640 - 644 of the
textbook.
Exercise 11.3.1: Definitions
Fill in the blanks to complete the following sentences.
Let G be an (undirected) graph with vertices v1, v2, ¼, vn in the given order. The adjacency
matrix of G is the matrix A = [aij] over the set of nonnegative
integers such that aij = the number of edges
connecting vi and vj for all i, j = 1, 2, ¼, n.
In other words, the adjacency matrix of G is the matrix A = [aij] over the set
of nonnegative integers such that
| aij = |
{ |
r if there exist r edges
connecting vi and vj |
| 0 otherwise |
Exercise 11.3.2: Examples
You should attempt all these exercises yourself, using the textbook as an aid. Once you
have attempted each question, check your answers by following the appropriate links. If
you are stuck on a question, choose the link that gives you a hint and then try the
question again.
1. Find the adjacency matrix for the following graph.

Hint
Full solution
2. Another useful way of describing a graph is by using an incidence matrix. Let
G be a graph with vertex set V(G) = v1, v2, ¼,
vr and edge set
E(G) = e1, e2, ¼, es.
An incidence matrix for the graph G is a matrix N = (nij), of
size r × s, with a row corresponding to each vertex of the graph and a column
corresponding to each edge of the graph. The entries, nij, of the
incidence matrix for graph G are
| nij = |
{ |
2 if edge ej is a loop on vertex vi, |
| 1 if edge ej is an edge connecting vertex vi
to some other vertex, |
| 0 otherwise. |
Find the incidence matrix for the following graph.

Hint
Full solution
3. Use incidence matrices to prove that for any graph G with vertices v1, v2, ¼, vn and e edges,
Hint
Full solution
Section 11.5
Trees
The following solutions make use of information found on pages 664 - 674 of the
textbook.
Exercise 11.5.1: Definitions
Fill in the blanks to complete the following sentences.
- A graph is said to be circuit-free if, and
only if, it has no nontrivial circuits.
A graph is called a tree
if, and only if, it is circuit-free and
connected.
A trivial
tree is a graph that consists of
a single vertex.
A graph is called a forest if, and only if,
it
is circuit-free.
Hence a forest is a (not necessarily connected) graph which may
be thought of as a union of trees.
- Theorem Let n be a positive integer and G a tree
on n vertices. Then G has n-1 edges.
- A finite connected simple graph G with n vertices is a tree if,
and only if, it has
exactly n-1 edges.
Exercise 11.5.2: Examples
You should attempt all these exercises yourself, using the textbook as an aid. Once you
have attempted each question, check your answers by following the appropriate links. If
you are stuck on a question, choose the link that gives you a hint and then try the
question again.
1. Which of the following graphs are trees?
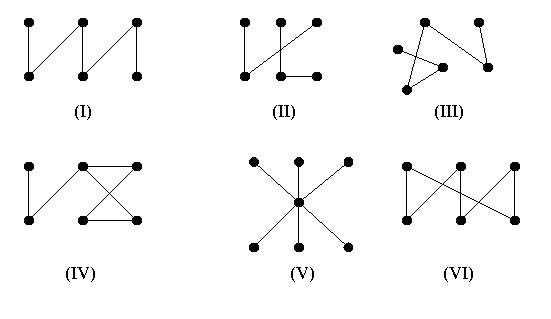
Hint
Full solution
2. Which complete bipartite graphs Km,n, where m and n are positive
integers, are trees?
Hint
Full solution
3. A tree has precisely five vertices of degree 1 and one vertex of degree 5.
a) Find the degrees of all the vertices in this tree.
b) Draw any two such trees, one with eight vertices and one with six vertices.
Hint
Full solution
Back to workbook solution page









