Solution for Section 4.2 Question 2b

2b)

Let P(n) be the claim: n

     1    

j (j + 1)

=

    n   

n + 1
for all integers n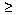geq.jpg (602 bytes)1.
S
j = 1
P(1) is the statement: 1

     1      

j (j + 1)

=

   1  

1 + 1
S
j = 1
P(k) is the statement: k

     1     

j (j + 1)

=

    k    

k + 1
S
i = 1
P(k+1) is the statement: k + 1

     1     

j (j + 1)

=

  k + 1 

k + 2
S
i = 1

For a proof by induction, you first need to check that the statement P(1) is true. Then assume that P(k) is true and use this to show that P(k + 1) is true.

 

The statement P(1) is true since 1

     1    

1 (1 + 1)

=

   1  

=

1

1 · 2

2
S
i = 1

Now assume that the statement P(k) is true. We now need to show that the left-hand side of P(k+1) is equal to the right-hand side of P(k+1).

L.H.S of P(k+1)

=

 k + 1

     1    

j (j + 1)
S
i = 1

=

 k

     1    

j (j + 1)

+

          1          

(k + 1) (k + 2)
S
i = 1
=

    k   

+

          1          

(since we are assuming that P(k) is true)

k + 1

(k + 1) (k + 2)
=

  k (k + 2) + 1 

(k + 1) (k + 2)
=

    k2 + 2k + 1  

(k + 1) (k + 2)
=

     (k + 1)2   

(k + 1) (k + 2)
=

  k + 1 

k + 2
= R.H.S. of P(k+1)

 

Therefore, for all integers n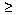geq.jpg (602 bytes)1, n

     1    

j (j + 1)

=

    n   

n + 1
S
j = 1

Back to Section 4.2