
By Diane Donovan
Hi Club Infinity members, we thought you might be interested in the following method for solving SUDOKU type puzzles.
To make it easier to understand we have applied our algorithm to a small 4 x 4 puzzle, but you can apply the same technique to larger puzzles.
So first a statement of the puzzle.

RULES: The symbols 1, 2, 3, 4 have to be entered into the empty cells in the 4 x 4 square shown below, in such a way that each symbol occurs once in every row, once in every column and once in every coloured 2 x 2 sub-square.
One good method for finding a solution to this puzzle is to take each empty cell and write a list of possible symbols which can be placed in that empty cell. We build these lists by using the facts that each symbol can occur once in every row, once in every column and once in every 2 x 2 sub-square.
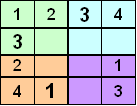
For this example the list of possible symbols for the empty cells are shown in the array on the right. The dark coloured squares indicate that these cells have already been filled in.

![]()
We see immediately that the two empty corner cells must contain the symbol 4. And so we update our square and then update our lists for the remaining empty cells.

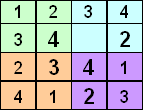
We can now see that two more 1’s are forced and so are two more 3’s. So we update our square and, if we wanted to, we could easily complete the square at this point. But for the sake of executing our algorithm we will update our lists and continue the process.

Leading to:

And so our solution is:
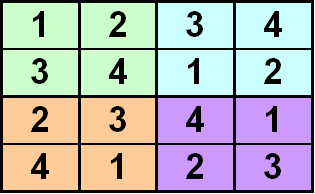

What if we change the rules of the puzzle?
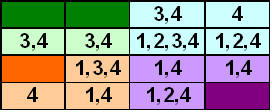
NEW RULES: The symbols 1, 2, 3, 4 have to be entered into the empty cells in the 4 x 4 square shown below, in such a way that each symbol occurs once in every row, once in every column, once in each square coloured green, once in each square coloured blue, once in each square coloured orange and once in each square coloured purple.

For this square the list of possible symbols (don’t forget to use your rules) which can be placed in each empty cell is:

Straight away we see that three 2’s which are forced in cells in rows one, two and three, and we can update our square as follows.
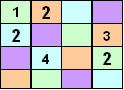
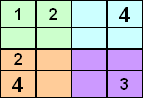
Finally updating the list of possible symbols which may now be placed in the empty cells gives:

It is now obvious that our solution must be:
|
1 |
2 |
3 |
4 |
|
2 |
1 |
4 |
3 |
|
3 |
4 |
1 |
2 |
|
4 |
3 |
2 |
1 |

The last square shown above is an example of an orthogonal latin square.
For now we will define an orthogonal latin square as an n x n array, where the cells are coloured using n colours in such a way that each colour occurs once in each row and once in each column, and we place the symbols 1 to n in the cells in in such a way that each symbol occurs once in every row, once in every column, and for each colour and each symbol, there is precisely one cell shaded with that colour and containing that symbol.
If you check the 4 x 4 square above you will see that it satisfies this definition for n = 4.
Now lets make it even harder. Look at the following square
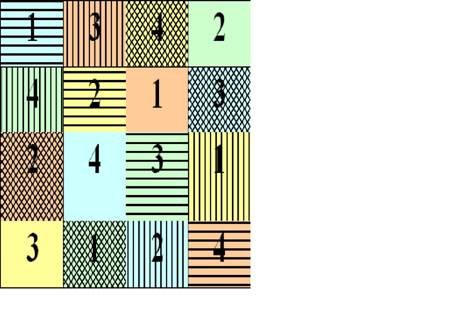
It satisfies the definition of an orthogonal latin square, but it has the added property that if we look at the patterns on the cells, then each pattern occurs once in every row, once in every column. Further for each pattern and each symbol there is precisely one cell which contains that combination, and for each pattern and each colour there is precisely one cell which contains that combination.
Mathematically we think of pulling this array apart into three arrays as shown
|
1 |
3 |
4 |
2 |
|
4 |
2 |
1 |
3 |
|
2 |
4 |
3 |
1 |
|
3 |
1 |
2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Together we say these three squares form a set of three mutually orthogonal latin squares.
It can be proven mathematically that for arrays of size 5 x 5, 7 x 7, 8 x 8, 9 x 9 and N x N, where N is greater than 10, we can always find three arrays which have the above properties. It is also know that it is not possible to find 3 such 6 x 6 arrays.
But nobody knows if we can find three such 10 x 10 arrays? This is an open question which many researchers are studying. If you want to know more about this important problem then look up these websites.
