
A summary of my research for a non-specialist audience is featured in the journal International Innovation, July 2013, pp 65-67 (pdf). This Public Lecture on randomness shows how we can better understand it through mathematics. Python files may be found here.
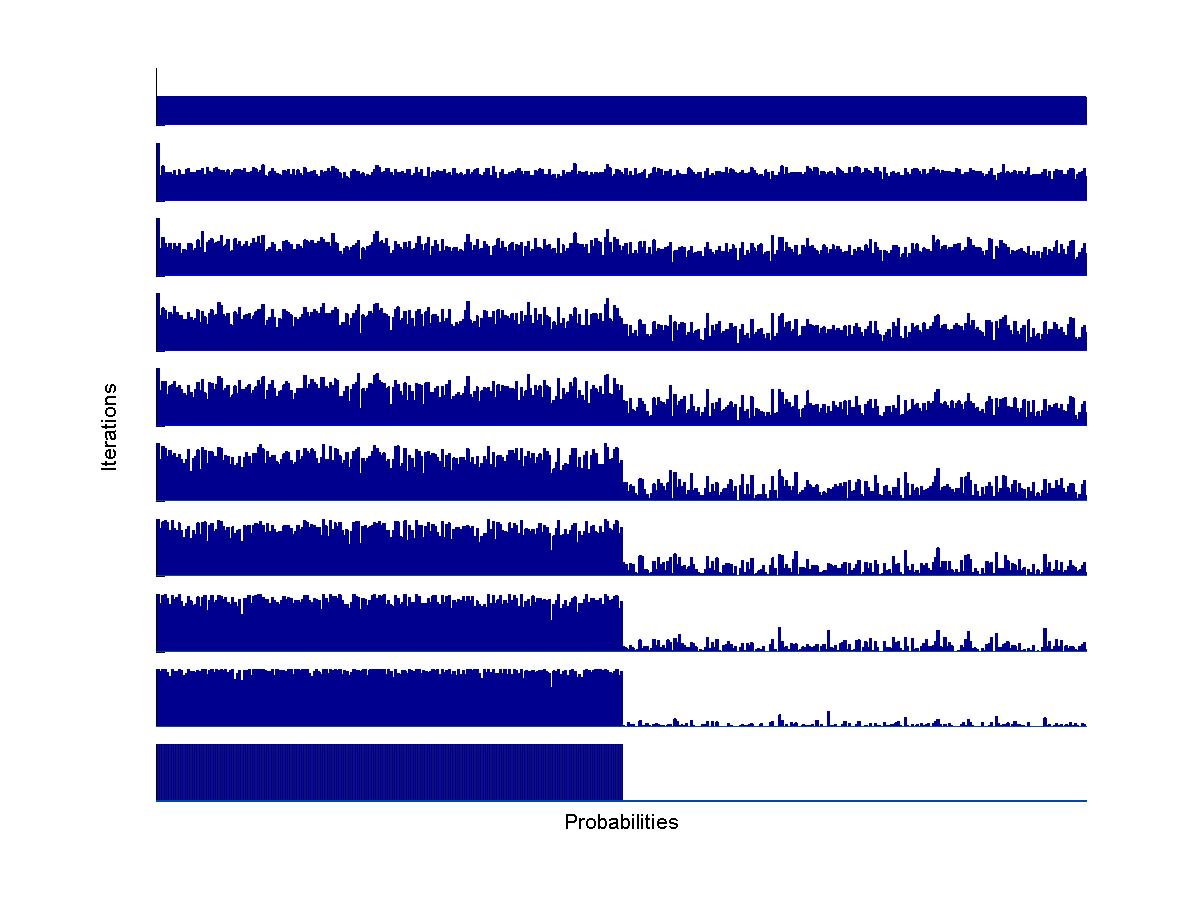
The max-cut problem is a famous "hard" combinatorial optimization problem where the nodes of a network are to be partioned into two groups so as to optimize the number of connections (or weights) between the two groups. The CE method is very well suited to solve the max-cut problem. Below is an illustration of the CE method. With each node in the network we associate a probability, and this probabilty is updated at each iteration to converge to either 0 or 1, depending on whether the node should be put in group 0 or 1. In the example below, with 400 nodes, the optimal partition is to put nodes 1 - 200 in the first group and nodes 201 - 400 in the second.
The Wiener process or Brownian motion is one of the most important random processes. It can be seen as a continuous version of a random walk process. What is the best/easiest way to generate Wiener processes on general surfaces? Below is a picture of the path of a Wiener process on the torus.

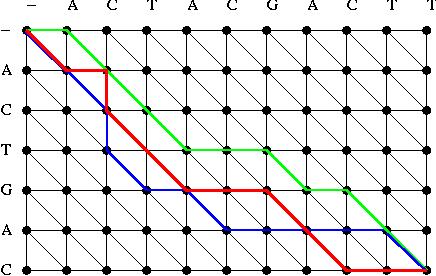
| DNA Sequencing We can use randomised algorithms to align DNA and protein sequences. Generate random path through the network, calculate the score for each path and use that to update the transition probabilities. The algorithm converges to the optimal path that corresponds to the minimal score alignment. |
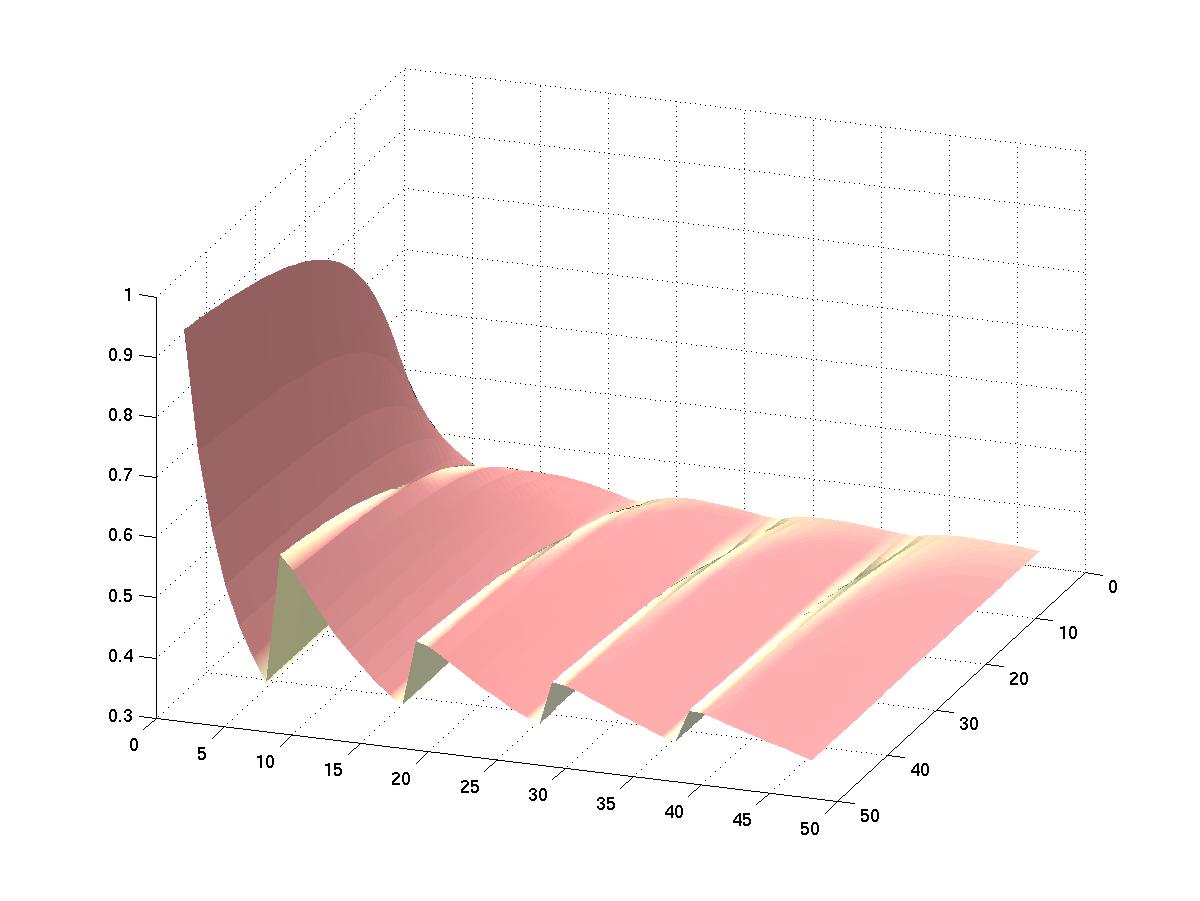
Effective Bandwidth In a packet switched telecommunication network the Effective Bandwidth of a connection describes the link capacity (bits per second) needed to transmit the packets with a guaranteed Quality of Service. Below, the effective bandwidth surface for a periodic transmission source is depicted. |
 |
 |