Today we will examine the concepts of continuity of surfaces.

1. Let’s begin with some background. A function f(x,y) has a limit L at the point (a,b) if the absolute value of the difference between | f(x,y) – L| is less than some small constant, called e, over a rectangular region (a - d < x < a + d) and (b - d < y < b + d) surrounding the point (a,b) where d is a number that you pick. Consider the function

,

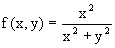Evaluate the function at the point (2,3). Now make a plot of the surface given by P(x,y) = |f(x,y)-f(2,3)| in the region surrounding (2,3). Use d = 0.1 and from the figure pick the smallest e that you can. Repeat the procedure for d = 0.01.

Plot the contour diagrams with the ezcontour command.

Repeat question 1 around the point (0,0). Note that at (0,0) f(x,y) is undefined. For this instance just use P(x,y)=| f(x,y)|.

You will see that the surface has a strange folded shape around (0,0).

2. You can understand what is happening as you approach the origin along a line y = kx, where k is a given slope, by substituting this into the equation above and then letting x go to 0. Make a graph of the resulting values of f(0,0) versus the range of slope values –10 < k < 10.