MATH1052 Semester 1 2001
Computer Project 1
This project deals with the maxima of surfaces in 3-dimensional
space. You will need to answer a series of questions and submit the results
for assessment. For all figures you create using Matlab, you need to also
submit the commands that you used to create the output. Working must be
shown for all calculations done by hand.
PART A
1. Create and print a graph which clearly shows the intersection
of the surfaces
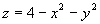 (1)
(1)
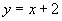 (2)
(2)
over the domain 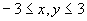 .
.
2. By hand, substitute (2) into (1) and determine the
maximum value of (1) subject to the constraint given by (2). (You should
be able to check the accuracy of your calculation from the graph you produce
above.)
3. In the 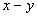 plane, plot on the same graph equation (2) and a contour diagram for (1)
at the values
plane, plot on the same graph equation (2) and a contour diagram for (1)
at the values 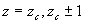 where
where 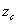 is the constrained maximum value found in part 2. Again, make this plot
over the domain
is the constrained maximum value found in part 2. Again, make this plot
over the domain 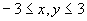
.
PART B
For functions of one variable it is impossible for a continuous
function to have two local maxima and no local minimum. In this question
we will see that this is not the case for functions of many variables.
1. Use the ezplot and hold on commands to
make a contour diagram for the function
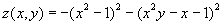
for the values z = -2, -0.5, -0.1, with domain
-2 < x < 2, -1 < y < 3.
2. By hand, show that z has only two critical points
(1, 2) and (-1, 0)
and they are both local maxima.
3. Plot the line y=x+1 on your contour diagram.
(Note that the two critical points lie on this line.)
4. Now substitute y=x+1 into z(x,
y)
to obtain a new function of one variable w(x)=z(x,
x+1).
We already know that w has local maxima at
x= -1, 1. Determine the value of x between
- 1 and 1 for which w has a local minimum. (HINT: you will not be
able to find the solution
exactly. Use the xzero command in 10.2 of the
Matlab notes.)
5. Determine the minimum value of w(x) and
plot the contour for z(x, y) at this value. What do
you notice about this curve and the line y=x+1? Explain why
it is possible to travel along the line y=x+1 from the local
maximum for z at (-1,0) to the other local maximum at (-1,2), without
passing through a local minimum for z.
![]() (1)
(1)
![]() (2)
(2)
![]() .
.
![]() plane, plot on the same graph equation (2) and a contour diagram for (1)
at the values
plane, plot on the same graph equation (2) and a contour diagram for (1)
at the values ![]() where
where ![]() is the constrained maximum value found in part 2. Again, make this plot
over the domain
is the constrained maximum value found in part 2. Again, make this plot
over the domain ![]()