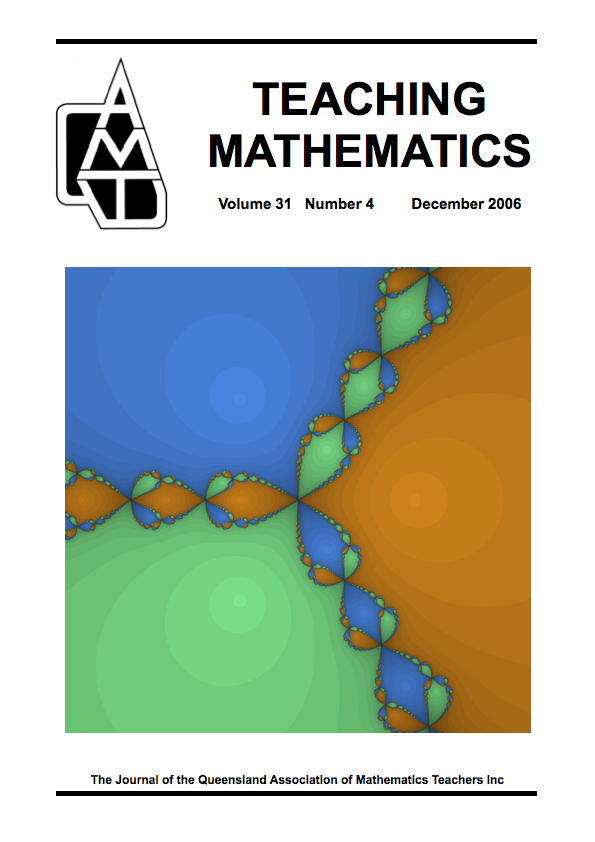
This front cover shows an image of a Newton fractal, here generated from the convergence of Newton's method used for finding the roots of the polynomial z³ - 1 in the complex plane. The image shows the section of the plane from -2-2i (bottom left) to +2+2i (top right) with the origin in the centre. The colour of each point in the plane indicates which of the three roots of the polynomial Newton's method converges to when started at that point. The intensity of the colour indicates how quickly the method converges, with darker regions indicating slower convergence. The brightest regions are around the three roots themselves: +1 and -(1/2) ± (√3/2)i.