Similar Markov chains
Phil Pollett
Abstract:
In a recent paper (J. Appl. Probab. 37 (2000), 835-849) Lenin,
Parthasarathy, Scheinhardt and van Doorn introduced the idea of
similarity in the context of birth-death processes. I will examine the
extent to which their results can be extended to arbitrary
continuous-time Markov chains over a countable state space S. Two such
chains are said to be similar
if their transition functions P and
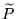 satisfy
satisfy
for some collection of positive constants cij, 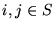 (pij(t) can be interpretted as the probability of moving from state
i to state j in time t). I will prove, under a variety of
conditions, that similar chains are strongly similar in the
following sense:
(pij(t) can be interpretted as the probability of moving from state
i to state j in time t). I will prove, under a variety of
conditions, that similar chains are strongly similar in the
following sense:
for positive constants
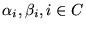 .
I will
also show that minimal chains are strongly similar if and only if the
corresponding transition-rate matrices are also strongly similar in an
obvious sense. This gives rise to a general framework for constructing
families of strongly similar chains, one which allows us to construct
all such chains in the irreducible case. I will draw heavily on the
"Vere-Jones theory" of Markov chains, which provides the basic
framework for studying questions concerning the convergence of Markov
transition probabilities and their associated spectral properties.
.
I will
also show that minimal chains are strongly similar if and only if the
corresponding transition-rate matrices are also strongly similar in an
obvious sense. This gives rise to a general framework for constructing
families of strongly similar chains, one which allows us to construct
all such chains in the irreducible case. I will draw heavily on the
"Vere-Jones theory" of Markov chains, which provides the basic
framework for studying questions concerning the convergence of Markov
transition probabilities and their associated spectral properties.
Acknowledgement:
This worked was funded by
the Australian Research Council.
The author:
-
Phil Pollett,
Department of Mathematics,
The University of Queensland.
pkp@maths.uq.edu.au
Last modified: 17th April 2001
![]() satisfy
satisfy