SIMILAR MARKOV CHAINS
by
Phil Pollett

Department of Mathematics
The University of Queensland
SIMILAR MARKOV CHAINS
by
Phil Pollett

Department of Mathematics
The University of Queensland
There is an accompanying paper:
| Pollett, P.K. (2001) Similar Markov chains. Journal of Applied Probability 38A (to appear). |
From that paper:
| "I was introduced to David Vere-Jones' work by another of my mentors, Charles Pearce, whose lively undergraduate lectures on the Vere-Jones theory did much to convince me that I should follow a probability path. David's work has been a constant source of inspiration to me and I continue to benefit from our fruitful and enjoyable collaborations. I am grateful to him personally for his advice, encouragement and friendship over many years and I therefore take great pleasure in dedicating this short note to him." |
From those lectures:

MAIN REFERENCES
Convergence of Markov transition probabilities and their spectral properties
1. Vere-Jones, D. Geometric ergodicity in denumerable Markov chains. Quart. J. Math. Oxford Ser. 2 13 (1962) 7-28.
2. Vere-Jones, D. On the spectra of some linear operators associated with queueing systems. Z. Wahrscheinlichkeitstheorie und Verw. Gebiete 2 (1963) 12-21.
3. Vere-Jones, D. Ergodic properties of nonnegative matrices. I. Pacific J. Math. 22 (1967) 361-386.
4. Vere-Jones, D. Ergodic properties of nonnegative matrices. II. Pacific J. Math. 26 (1968) 601-620.
Classification of transient Markov chains and quasi-stationary distributions
5. Seneta, E.; Vere-Jones, D. On quasi-stationary distributions in discrete-time Markov chains with a denumerable infinity of states. J. Appl. Probability 3 (1966) 403-434.
6. Vere-Jones, D. Some limit theorems for evanescent processes. Austral. J. Statist. 11 (1969) 67-78.
Related work
7. Vere-Jones, D.; Kendall, David G. A commutativity problem in the theory of Markov chains. Teor. Veroyatnost. i Primenen. 4 (1959) 97-100.
8. Vere-Jones, D. A rate of convergence problem in the theory of queues. Teor. Verojatnost. i Primenen. 9 (1964) 104-112.
9. Vere-Jones, D. Note on a theorem of Kingman and a theorem of Chung. Ann. Math. Statist. 37 (1966) 1844-1846.
10. Heathcote, C. R.; Seneta, E.; Vere-Jones, D. A refinement of two theorems in the theory of branching processes. Teor. Verojatnost. i Primenen. 12 (1967) 341-346.
11. Rubin, H.; Vere-Jones, D. Domains of attraction for the subcritical Galton-Watson branching process. J. Appl. Probability 5 (1968) 216-219.
12. Seneta, E.; Vere-Jones, D. On the asymptotic behaviour of subcritical branching processes with continuous state space. Z. Wahrscheinlichkeitstheorie und Verw. Gebiete 10 (1968) 212-225.
13. Fahady, K. S.; Quine, M. P.; Vere-Jones, D. Heavy traffic approximations for the Galton-Watson process. Advances in Appl. Probability 3 (1971) 282-300.
14. Pollett, P. K.; Vere-Jones, D. A note on evanescent processes. Austral. J. Statist. 34 (1992), no. 3, 531-536.
Important early work on quasi-stationary distributions
Yaglom, A.M. Certain limit theorems of the theory of branching processes (Russian) Doklady Akad. Nauk SSSR (N.S.) 56 (1947) 795-798.
Bartlett, M.S. Deterministic and stochastic models for recurrent epidemics. Proceedings of the Third Berkeley Symposium on Mathematical Statistics and Probability, 1954-1955, Vol. IV, pp. 81-109. University of California Press, Berkeley and Los Angeles, 1956.
Bartlett, M.S. Stochastic population models in ecology and epidemiology. Methuen's Monographs on Applied Probability and Statistics Methuen & Co., Ltd., London; John Wiley & Sons, Inc., New York, 1960.
Darroch, J. N.; Seneta, E. On quasi-stationary distributions in absorbing discrete-time finite Markov chains. J. Appl. Probability 2 (1965) 88-100.
Darroch, J. N.; Seneta, E. On quasi-stationary distributions in absorbing continuous-time finite Markov chains. J. Appl. Probability 4 (1967) 192-196.
Important early work on quasi-stationary distributions
Mandl, Petr Sur le comportement asymptotique des probabilités dans les ensembles des états d'une chaîne de Markov homogène (Russian) Casopis Pest. Mat. 84 (1959) 140-149.
Mandl, Petr On the asymptotic behaviour of probabilities within groups of states of a homogeneous Markov process (Czech) Casopis Pest. Mat. 85 (1960) 448-456.
Ewens, W.J. The diffusion equation and a pseudo-distrib-ution in genetics. J. Roy. Statist. Soc., Ser B 25 (1963) 405-412.
Kingman, J.F.C. The exponential decay of Markov transition probabilities. Proc. London Math. Soc. 13 (1963) 337-358.
Ewens, W.J. The pseudo-transient distribution and its uses in genetics. J. Appl. Probab. 1 (1964) 141-156.
Seneta, E. Quasi-stationary distributions and time-rever-sion in genetics. (With discussion) J. Roy. Statist. Soc. Ser. B 28 (1966) 253-277.
Seneta, E. Quasi-stationary behaviour in the random walk with continuous time. Austral. J. Statist. 8 (1966) 92-98.
DISCRETE-TIME CHAINS
Setting:
![]() , a time-homogeneous Markov chain taking
values in a countable set S with transition probabilities
, a time-homogeneous Markov chain taking
values in a countable set S with transition probabilities
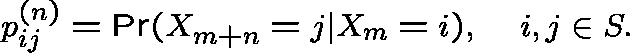
Let C be any irreducible and (for simplicity) aperiodic class.
DVJ1:
For ![]() ,
,
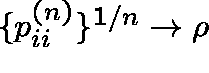 as
as ![]() . The limit
. The limit ![]() does not depend on i
and it satisfies
does not depend on i
and it satisfies ![]() .
Moreover,
.
Moreover, 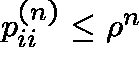 and indeed,
for
and indeed,
for ![]() ,
, 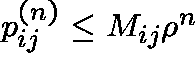 ,
where
,
where ![]() .
.
(If C is recurrent, 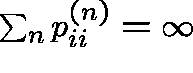 implies
implies ![]() .
When C is transient, we can have
.
When C is transient, we can have ![]() , or,
, or,
![]() , which is called geometric ergodicity.)
, which is called geometric ergodicity.)
DVJ2:
For any real r>0, the series
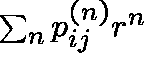 ,
, ![]() , converge or diverge together;
in particular, they have the same radius
of convergence R, and
, converge or diverge together;
in particular, they have the same radius
of convergence R, and ![]() . And, all or none of the sequences
. And, all or none of the sequences
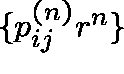 tend to zero.
tend to zero.
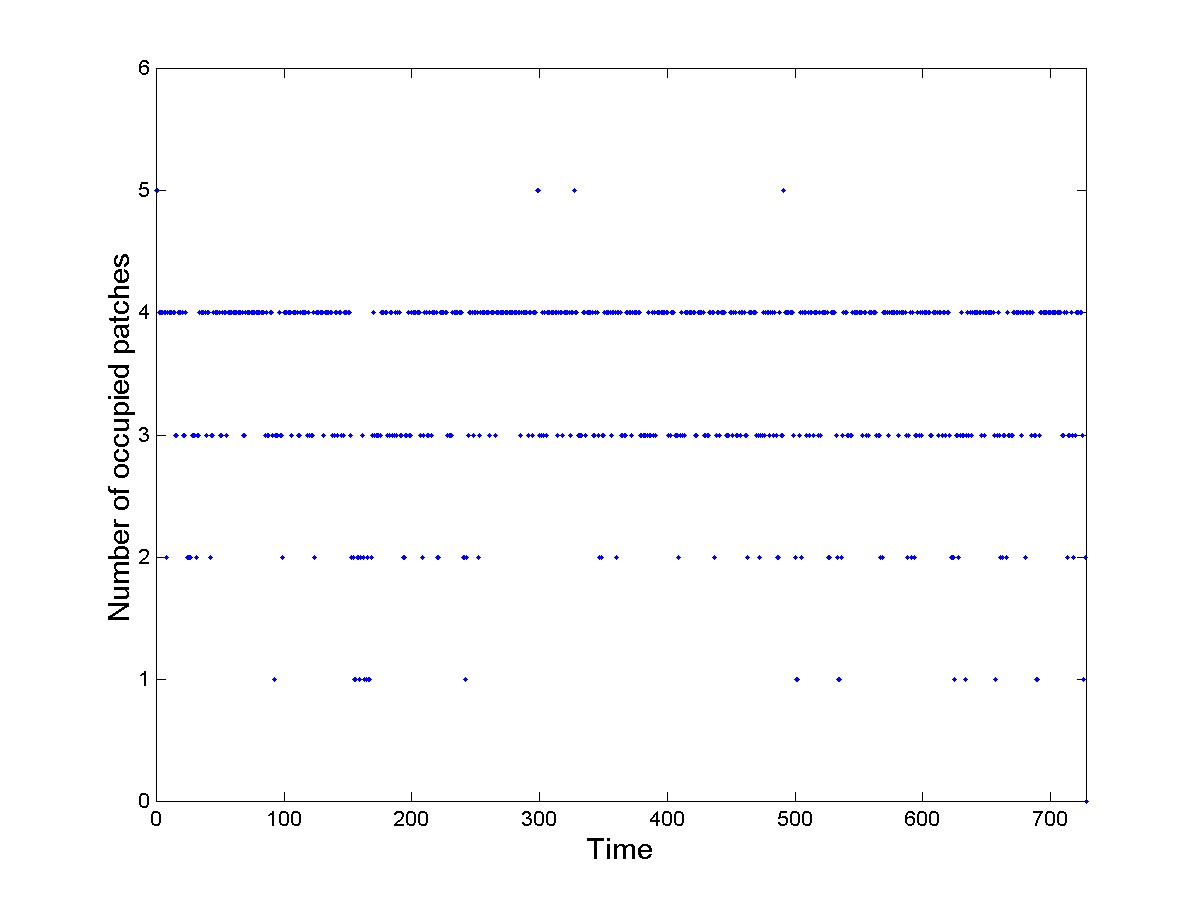
Figure 1. Simulation of a metapopulation model.
(Download the following image (as postscript)):

Figure 2. State transition diagram for
epidemic model.
(Download the following image (as postscript)):
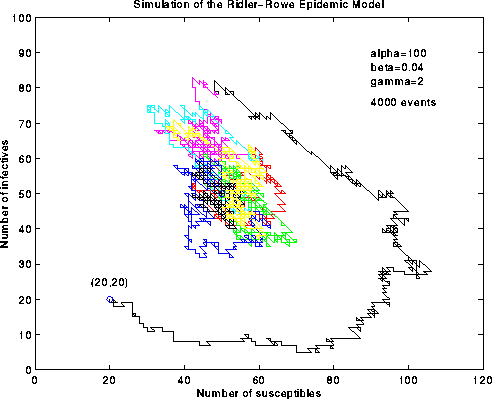
Figure 3. Simulation of the epidemic model
[Simulation |
java code]
(Download the following image (as postscript)):
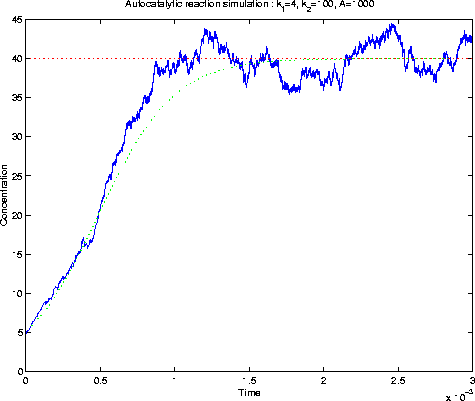
Figure 4. Auto-catalytic reaction simulation
[Simulation |
java code]
(Download the following image (as postscript)):
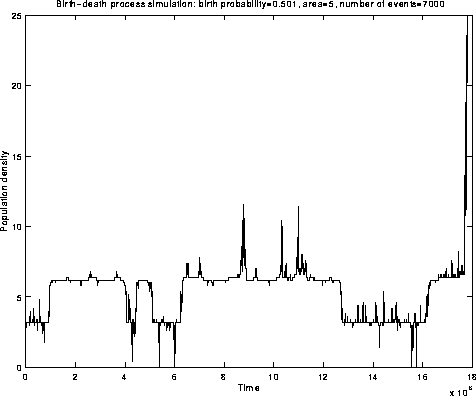
Figure 5. Quasistationarity of an explosive population process
[Simulation
|
java code]
TRANSIENT CHAINS
The key to unlocking this "quasi-stationarity" is to examine the behaviour of the transition probabilities at the radius of convergence R.
Suppose that C is transient class
which is geometrically ergodic ( ![]() , R>1).
Although
, R>1).
Although 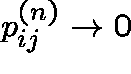 , it might be true that
, it might be true that
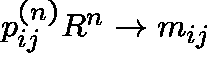 , where
, where ![]() .
How does this help?
.
How does this help?
For ![]() ,
,
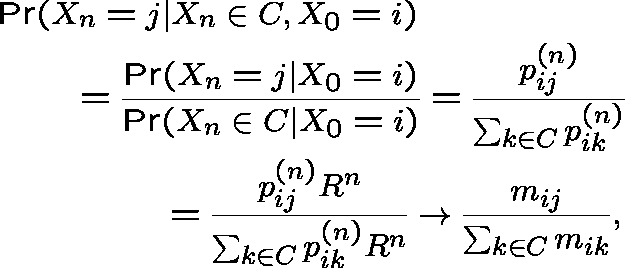
provided that we can justify taking limit under summation.
DVJ3:
C is said to be
R-transient or
R-recurrent
according as
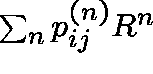 converges or diverges.
If C is R-recurrent, then it is said to be
R-positive or
R-null
according to whether the limit of
converges or diverges.
If C is R-recurrent, then it is said to be
R-positive or
R-null
according to whether the limit of
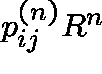 is positive or zero.
is positive or zero.
DVJ4:
If C is R-recurrent, then, for ![]() , the inequalities
, the inequalities
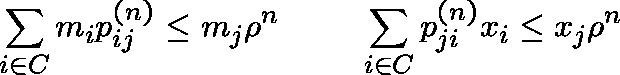
have unique positive solutions ![]() and
and ![]() and indeed
they are eigenvectors:
and indeed
they are eigenvectors:
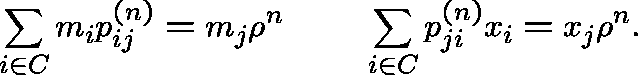
C is then R-positive recurrent if and only if
![]() , in which case
, in which case
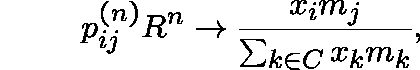
and, if ![]() , then
, then
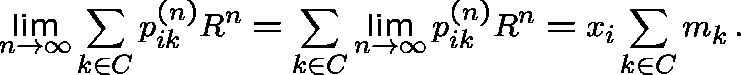
AND FINALLY
S-DVJ:
If C is R-positive recurrent and the left-eigenvector
satisfies ![]() , then the limiting conditional
(or quasi-stationary) distribution exists:
as
, then the limiting conditional
(or quasi-stationary) distribution exists:
as ![]() ,
,
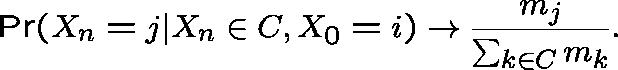
... AND MUCH MORE
Other kinds of QSD, more general and more precise statements, continuous-time chains, general state spaces, numerical methods and in particular truncation methods, MCMC, countless applications of QSDs: chemical kinetics, population biology, ecology, epidemiology, reliability, telecommunications. A full bibliography is maintained at my web site:
http://www.maths.uq.edu.au/~pkp/research.html
(Download the following image (as postscript)):
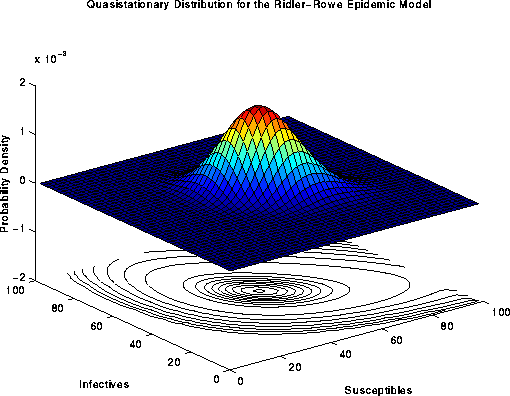
Figure 6. Surface plot of the quasistationary distribution
for the epidemic model
SIMILAR MARKOV CHAINS
New setting:
![]() , a time-homogeneous Markov chain
in continuous time taking
values in a countable set S, with transition function
, a time-homogeneous Markov chain
in continuous time taking
values in a countable set S, with transition function
![]() , where
, where
![]()
Assuming that ![]() (standard),
the transitions rates are defined by
(standard),
the transitions rates are defined by
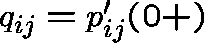 .
Set
.
Set ![]() and assume
and assume ![]() (stable).
(stable).
Definition:
Two such chains X and ![]() are said to be similar if
their transition functions, P and
are said to be similar if
their transition functions, P and ![]() , satisfy
, satisfy
![]() ,
, ![]() , t>0,
for some collection of positive constants
, t>0,
for some collection of positive constants ![]() ,
, ![]() .
.
Immediate consequences of the definition:
Since both chains are standard,
![]() and the transition rates must satisfy
and the transition rates must satisfy
![]() , in particular,
, in particular, ![]() .
They share the same irreducible classes and the same
classification of states.
.
They share the same irreducible classes and the same
classification of states.
Birth-death chains:
Lenin et al.![]() proved that for birth-death chains
the "similarity constants" must factorize as
proved that for birth-death chains
the "similarity constants" must factorize as
![]() . (Note that
. (Note that
![]() , since
, since ![]() .)
.)
Is this true more generally?
Definition:
Let C be a subset of S.
Two chains are said to be strongly similar over C if
![]() ,
, ![]() , t>0,
for some collection of positive constants
, t>0,
for some collection of positive constants ![]() ,
, ![]() .
.
Proposition:
If C is recurrent, then ![]() .
.
(Proof:
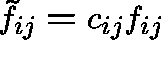 .)
.)
EXTENSION OF DJV THEORY
Kingman:
If C is irreducible, then, for each ![]() ,
,
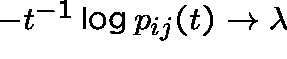 (
( ![]() ),
),
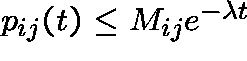 , for some
, for some ![]() ,
et cetera.
,
et cetera.
Definition:
C is said to be
![]() -transient or
-transient or
![]() -recurrent
according as
-recurrent
according as
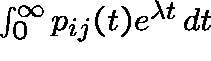 converges or diverges.
If C is
converges or diverges.
If C is ![]() -recurrent, then it is said to be
-recurrent, then it is said to be
![]() -positive or
-positive or
![]() -null
according to whether the limit of
-null
according to whether the limit of
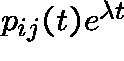 is positive or zero.
is positive or zero.
Theorem:
If C is ![]() -recurrent, then, for
-recurrent, then, for ![]() , the inequalities
, the inequalities
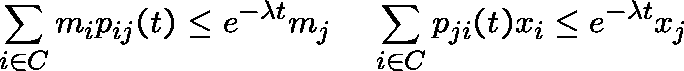
have unique positive solutions ![]() and
and ![]() and indeed
they are eigenvectors:
and indeed
they are eigenvectors:
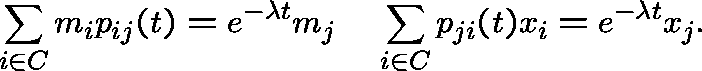
C is then ![]() -positive recurrent if and only if
-positive recurrent if and only if
![]() , in which case
, in which case
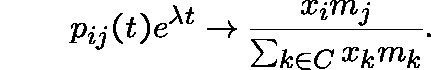
Suppose that P and ![]() are similar. They share the same
are similar. They share the same
![]() and the same
"
and the same
"![]() -classification".
-classification".
Theorem:
If C is a ![]() -positive
recurrent class, then P and
-positive
recurrent class, then P and ![]() are strongly similar over C. We may take
are strongly similar over C. We may take
![]() , where
, where ![]() and
and ![]() are the
essentially unique
are the
essentially unique ![]() -invariant measures (left eigenvectors)
on C for P and
for
-invariant measures (left eigenvectors)
on C for P and
for ![]() , respectively.
, respectively.
Proof:
Let ![]() in
in
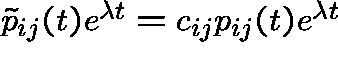 .
We get, in an obvious notation,
.
We get, in an obvious notation,
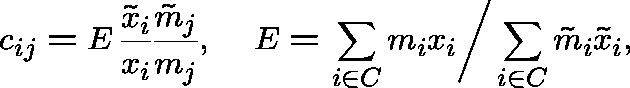
and, since ![]() , we have
, we have ![]() .
.
Again: Are similar chains always strongly similar?
In the ![]() -null recurrent case, it may still be possible to
deduce the desired factorization, for, although
-null recurrent case, it may still be possible to
deduce the desired factorization, for, although
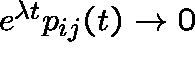 , it may be possible to
find a
, it may be possible to
find a ![]() such that
such that
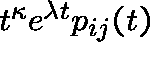 tends to a strictly positive limit.
(Similar chains will have the same
tends to a strictly positive limit.
(Similar chains will have the same ![]() .)
.)
Lemma:
Assume that C is ![]() -null recurrent and suppose
that there is a
-null recurrent and suppose
that there is a ![]() , which does not depend on i and
j, such that
, which does not depend on i and
j, such that 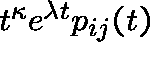 tends to a strictly
positive limit
tends to a strictly
positive limit ![]() for all
for all ![]() . Then, there is a positive
constant d such that
. Then, there is a positive
constant d such that ![]() ,
, ![]() , where
, where ![]() and
and ![]() are, respectively, the essentially unique
are, respectively, the essentially unique ![]() -invariant
measure and vector (left- and right-eigenvectors) on C for P.
-invariant
measure and vector (left- and right-eigenvectors) on C for P.
Remark:
Even in the ![]() -transient
case it might still be possible to find a
-transient
case it might still be possible to find a ![]() such that
such that 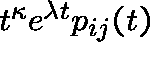 tends to
a positive limit, and for the conclusions to the lemma to hold good.
(Note that, by the usual irreducibility arguments,
tends to
a positive limit, and for the conclusions to the lemma to hold good.
(Note that, by the usual irreducibility arguments, ![]() will
be the same for all i and j in any given class.)
will
be the same for all i and j in any given class.)