M.S. Bebbington![]() ,
P.K. Pollett
,
P.K. Pollett![]() and
I. Ziedins
and
I. Ziedins![]()
Extended abstract
This paper is concerned with the performance evaluation of loss
networks. For the simplest networks, there are explicit analytical
formulae for the important measures of performance, but for networks
which involve some level of dynamic control, such as routing schemes
which make use of spare capacity, exact analytical
methods have had only limited success. Under several regimes, the
Erlang Fixed Point (EFP) method provides a good approximation for the
blocking probabilities, but when these regimes are not operative, the
method can perform badly because the key assumption of independent
blocking may not hold. We propose several new models which specifically
account for the dependencies between neighbouring links. We derive
approximations for the blocking probabilities with errors typically
![]() of that found using the EFP approximation. These are extended
to cases where admission controls, such as trunk reservation, are used.
of that found using the EFP approximation. These are extended
to cases where admission controls, such as trunk reservation, are used.
The assumption of independence between links which drives the EFP approximation holds under two limiting regimes. The first is one in which the topology of the network is held fixed, while capacities and arrival rates at links become large [4]; this has become known as the Kelly limiting regime, or (somewhat misleadingly) as the heavy traffic limit. Under the second limiting regime, called diverse routing, the number of links, and the number of routes which use these links, become large, while the capacities are held fixed and the arrival rate on any single route becomes small. Examples of this are star networks and fully-connected networks with alternate routing [2, 3, 5, 7, 8]. If neither regime is operative, the EFP method can perform badly: in particular, in highly linear networks and/or networks with low capacities. Further, adding controls to the network may destroy independence under otherwise favourable regimes. A particularly useful control is trunk reservation. Here, traffic streams are assigned priorities and calls are accepted only if the occupancies of links along their route are not above a given threshold, the size of which depends on the type of call. This widely used control mechanism is typically very robust to fluctuations in arrival rate and has the added advantage of eliminating pathological behaviour such as bistability [1]. With such a control operating in a network of reasonable size, links may be highly dependent and the equilibrium distribution will no longer have a product form, as it does for the corresponding uncontrolled network. Modelling dependencies in this context is thus critical.
We will focus attention on simple, highly linear networks, since here
the EFP approximation is expected to perform poorly. To illustrate our
methods, consider a loss network with K links forming a loop and each
link has the same capacity, C. There are two types of traffic: 1-link
routes (type-1 traffic) and 2-link routes comprising pairs of adjacent
links (type-2 traffic). Type-t traffic is offered at rate ![]() on
each type-t route. If
on
each type-t route. If ![]() is the common loss probability for
type-t calls, then the EFP approximation is
is the common loss probability for
type-t calls, then the EFP approximation is
![]()
where the Erlang Fixed Point B is the unique solution to
![]()
where ![]() is Erlang's Formula.
is Erlang's Formula.
A significant improvement in accuracy can be obtained by adapting methods
of Pallant [6]. The network is decomposed into independent
subnetworks and the stationary distribution is evaluated for each.
Consider a two-link subnetwork consisting of say links 1 and 2. There
are three routes: ![]() ,
, ![]() and
and ![]() . If
. If ![]() denotes the
number of calls on route r, then
denotes the
number of calls on route r, then ![]() is the number of
calls occupying capacity on link 1 but not on link 2,
is the number of
calls occupying capacity on link 1 but not on link 2, ![]() is the number occupying capacity on link 2 but not on
link 1, and,
is the number occupying capacity on link 2 but not on
link 1, and, ![]() is the number of calls occupying capacity
on both links.
The state space for the subnetwork is
is the number of calls occupying capacity
on both links.
The state space for the subnetwork is
![]() and the stationary distribution is
and the stationary distribution is
![]()
where G is a normalizing constant; we estimate B, the probability that a link adjacent to the two-link subnetwork is fully occupied, by
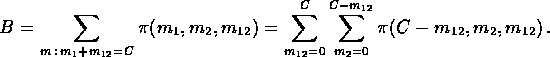
These expressions are used iteratively to determine a fixed point B
and then, as before, we set ![]() and
and ![]() .
.
Our second, and most accurate,
approximation uses additional knowledge of the state of a
given link in estimating the probability that the adjacent link is full.
We use state-dependent arrival rates, ![]() ,
,
![]() , where
, where ![]() is the probability that link K is fully
occupied, conditional on
is the probability that link K is fully
occupied, conditional on ![]() (
( ![]() is also the probability that
link 3 is fully occupied, conditional on
is also the probability that
link 3 is fully occupied, conditional on ![]() ), so that
), so that
![]()
Once ![]() is estimated and
is estimated and ![]() determined, we set
determined, we set
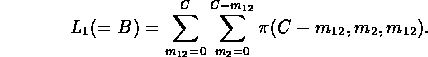
Similarly, ![]() can be expressed in terms of
can be expressed in terms of ![]() .
An estimate of
.
An estimate of ![]() is found by assuming that
is found by assuming that ![]() does not depend on
does not depend on ![]() . For
. For ![]() , we set
, we set
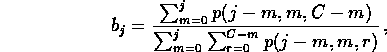
where
![]()
The dependence of ![]() on
on ![]() is due to the cyclic nature
of the network, but is expected to be slight for large networks.
is due to the cyclic nature
of the network, but is expected to be slight for large networks.
Full details of all fixed point methods will be described in the paper, including extensions to networks with trunk reservation. Detailed comparisons and error analysis will be provided for all methods.