Improved Fixed Point Methods for Loss Networks with Linear Structure
by
Mark Bebbington, Massey University
Phil Pollett, The University of Queensland
Ilze Ziedins, The University of Auckland

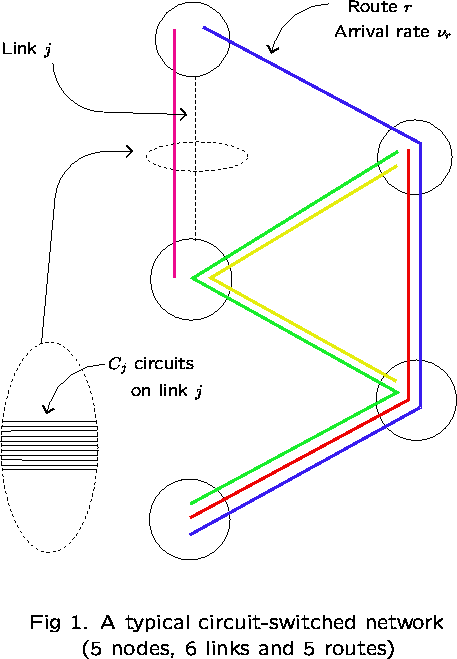
This consists of a group of nodes (locations),
K links (circuit groups),
![]() circuits comprising link j, and
circuits comprising link j, and
![]() - a collection of routes.
- a collection of routes.
Each route ![]() is a set of links. Calls using route r
are offered at rate
is a set of links. Calls using route r
are offered at rate ![]() as a Poisson stream,
and use
as a Poisson stream,
and use ![]() circuits from link j.
circuits from link j.
![]() indexes independent Poisson processes.
indexes independent Poisson processes.
Calls requesting route r are blocked and lost if, on
any link j, there are fewer than ![]() free circuits. Otherwise,
the call is connected and simultaneously holds
free circuits. Otherwise,
the call is connected and simultaneously holds ![]() circuits
on each link j for the duration of the call.
For simplicity, we shall take
circuits
on each link j for the duration of the call.
For simplicity, we shall take ![]() .
.
Call durations are iid exponential random variables with unit mean, and are independent of the arrival processes.
Let ![]() , where
, where ![]() is the number of
calls in progress using route r, let
is the number of
calls in progress using route r, let ![]() , and let
, and let
![]() .
.
The continuous-time Markov chain
![]() takes values in
takes values in
![]()
and has a unique stationary distribution given by
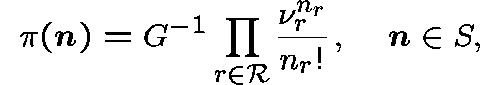
where ![]() is given by
is given by
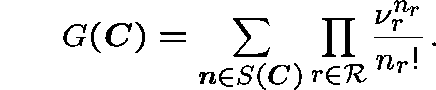
The stationary probability that a route-r call is blocked is given by
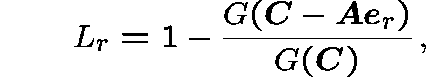
where ![]() is the unit vector from
is the unit vector from
![]() describing just one call in progress on route r
describing just one call in progress on route r
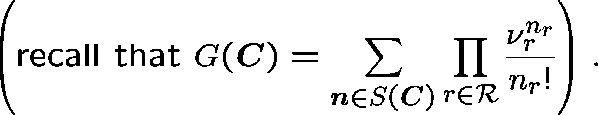
An explicit expression for ![]() !
!
However, the bad news is that
![]() can't usually be computed in polynomial time.
can't usually be computed in polynomial time.
For example, consider the trivial case of a fully-connected network
with all possible single-link routes ( ![]() ,
, ![]() )
and
)
and ![]() . Clearly,
. Clearly, 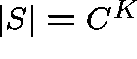 .
.
Theorem
(Kelly (1986)) There is a unique vector
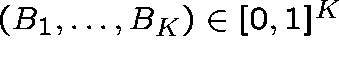 satisfying
satisfying
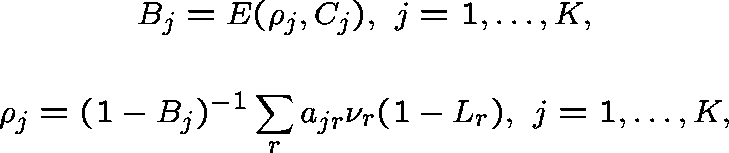
and
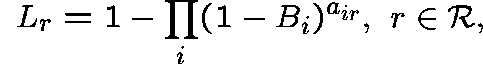
where
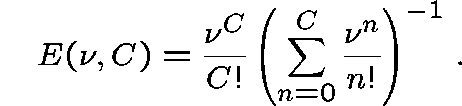
![]() is Erlang's Formula for the loss probability on
a single link with C circuits and Poisson traffic offered at
rate
is Erlang's Formula for the loss probability on
a single link with C circuits and Poisson traffic offered at
rate ![]() .
.
The celebrated Erlang Fixed Point Approximation is
obtained by using ![]() to estimate the probability that link j
is full, and using
to estimate the probability that link j
is full, and using ![]() to estimate the route-r blocking probability.
to estimate the route-r blocking probability.
(Independent blocking)
If links along route r were blocked independently (they are
clearly not) and if ![]() were the link-j blocking probability,
then
were the link-j blocking probability,
then ![]() would be the route-r blocking probability:
would be the route-r blocking probability:
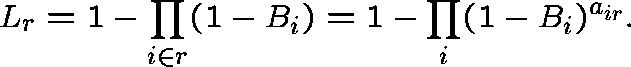
Carrying this rationale further, the traffic offered to
link j would be Poisson (at rate ![]() , say) and the
carried traffic
(that which is accepted) on link j would be
, say) and the
carried traffic
(that which is accepted) on link j would be
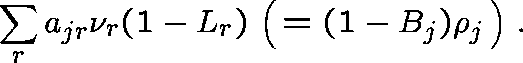
The Erlang Fixed Point Approximation stipulates that
the blocking probabilities ![]() should be
consistent with this level of carried traffic:
should be
consistent with this level of carried traffic:
![]()
The (unique) fixed point of the system
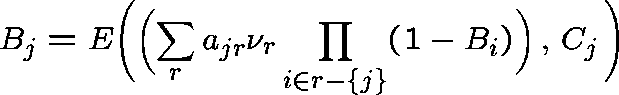
is called the Erlang Fixed Point.
Remarks The existence of a fixed point is easy to prove using
the Brouwer fixed point theorem; these equations determine a continuous
mapping from a compact convex set 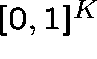 into itself. The uniqueness
(Kelly) is difficult to prove.
into itself. The uniqueness
(Kelly) is difficult to prove.
For more complex systems, there may be more than one fixed point. This may be associated with multiple stable states for the network. For example, in networks with Random Alternative Routing the system can fluctuate between a low blocking state, where calls are accepted readily, and a high blocking state, where the likelihood of a call being accepted can be quite low.
There are two limiting regimes under which the EFP is asymptotically valid:
Moderate loading (Kelly (1986)) Consider a sequence of networks indexed by N (arbitrary), and index the capacities and arrival rates accordingly:
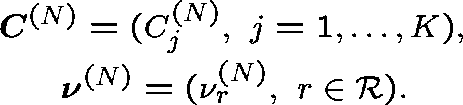
Theorem Suppose that as ![]()
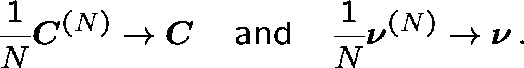
(Network topology fixed.)
If 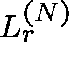 is the route-r loss probability, then, for each
is the route-r loss probability, then, for each
![]() ,
, 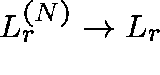 ,
where
,
where
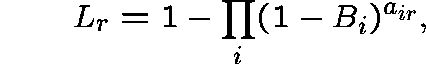
and ![]() is the Erlang Fixed Point determined by
is the Erlang Fixed Point determined by
![]() and
and ![]() .
.
Diverse routing (General formulation - Hunt (1990)) Consider a sequence of networks indexed by K (the number of links), and index the routing matrix and arrival rates accordingly:
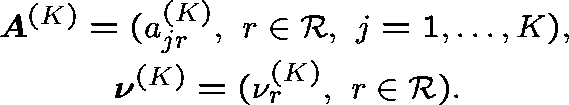
Suppose that
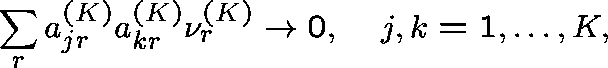
and
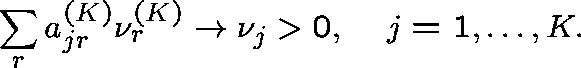
(Capacities fixed.)
The traffic along link j is moderate ( ![]() ),
but that which is common to any two links becomes small.
),
but that which is common to any two links becomes small.
There are no general results. Examples include star networks (Ziedins and Kelly (1989)) and networks with alternative routing (Gibbens, Hunt and Kelly (1990)); there are many more.
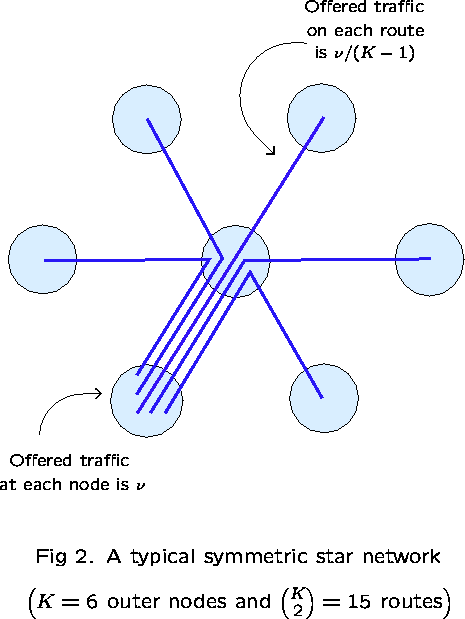
This consists of a collection of K outer nodes, which communicate
via a single central node. Take ![]() to be all
those routes consisting of a pair of links
(there are
to be all
those routes consisting of a pair of links
(there are ![]() of them).
Fix
of them).
Fix ![]() and take
and take ![]() for all
for all ![]() ,
and fix
,
and fix ![]() for all links
for all links ![]() .
.
Theorem
If ![]() is the common route loss probability, then
is the common route loss probability, then
![]() , given by
, given by
![]()
and B, the Erlang Fixed Point, is the unique solution to
![]()
where ![]() is Erlang's Formula.
is Erlang's Formula.
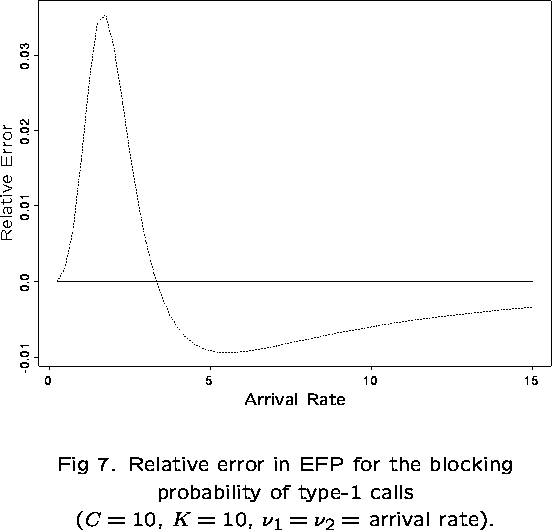
The EFP can perform badly if the network exhibits any of the following features:
- highly linear structure (lines and rings)
- low capacities
- priority controls (eg, trunk reservation)
In these cases, the independent blocking assumption may not be valid.
Can we model the link dependencies, and thus obtain improved fixed point methods?
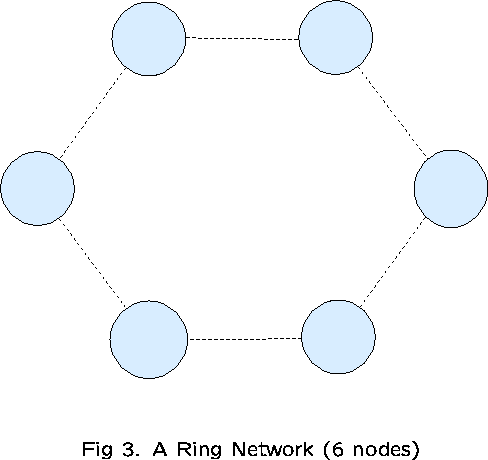
We shall examine a network consisting of K nodes with K links
which form a loop (see Figure 3). ![]() consist of all 1-link routes
(type-1 traffic), as well as all 2-link routes (type-2 traffic)
comprising pairs of adjacent links (2K routes in all). Type-t
traffic is offered at rate
consist of all 1-link routes
(type-1 traffic), as well as all 2-link routes (type-2 traffic)
comprising pairs of adjacent links (2K routes in all). Type-t
traffic is offered at rate ![]() on all type-t routes, for
on all type-t routes, for ![]() , and
, and ![]() for each link j.
for each link j.
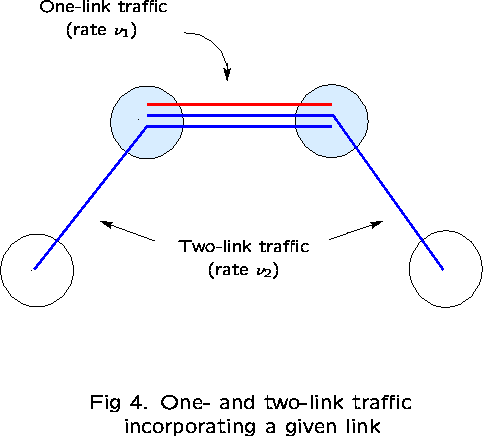
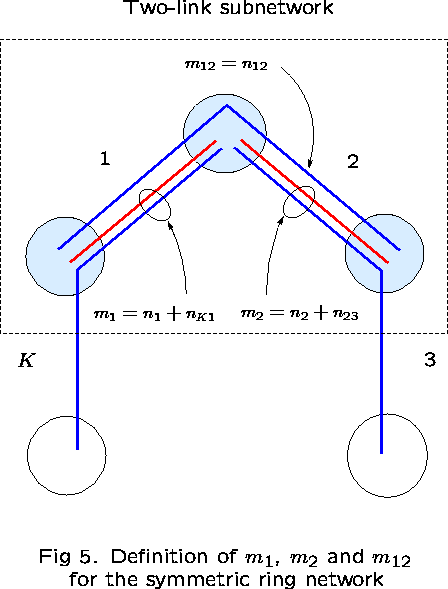
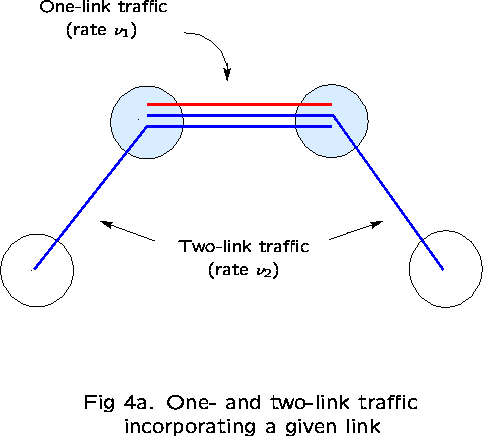
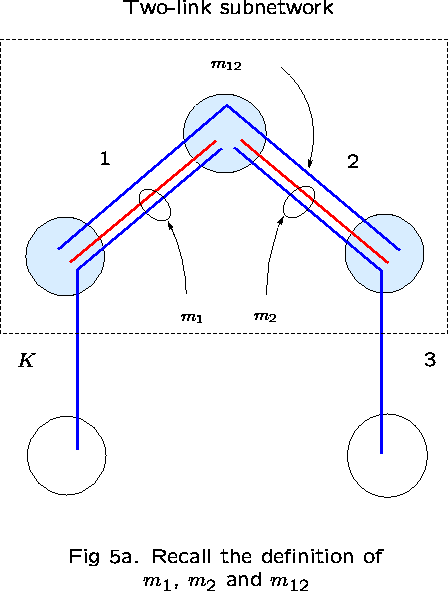
Take links 1 and 2 as ``reference'' links. The subnetwork consisting
of just these two links has three routes: ![]() .
Let
.
Let ![]() denote the number of calls on route r, for
denote the number of calls on route r, for ![]() .
Then,
.
Then, ![]() is the number of calls occupying capacity on
link 1 but not on link 2;
is the number of calls occupying capacity on
link 1 but not on link 2; ![]() is the number
occupying capacity on link 2 but not on link 1; and
is the number
occupying capacity on link 2 but not on link 1; and ![]() is the number of calls occupying capacity on both links (see
Figure 5).
is the number of calls occupying capacity on both links (see
Figure 5).
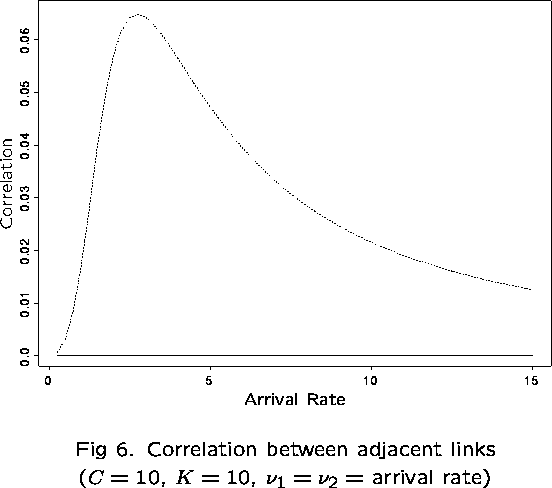
First examine the correlation between links 1 and 2, in particular,
![]()
If ![]() is the common loss probability for type-t calls,
for
is the common loss probability for type-t calls,
for ![]() , then the EFP approximation is
, then the EFP approximation is
![]()
where the Erlang Fixed Point B is the unique solution to
![]()
where ![]() is Erlang's Formula.
is Erlang's Formula.
This follows the work of Pallant (1992). The network is decomposed into independent subnetworks and the stationary distribution for each is evaluated.
The state space for the subnetwork is
![]()
and the stationary distribution is
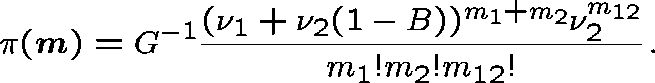
We estimate B, the probability that a link adjacent to the two-link subnetwork is fully occupied, by
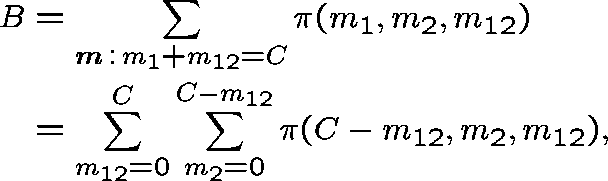
and use these expressions iteratively
to determine the ``correct'' value of ![]() , and hence B.
, and hence B.
Our second approximation uses additional knowledge of the state of a
given link in estimating the probability that the adjacent link is full.
We use state-dependent arrival rates, ![]() ,
,
![]() , where
, where ![]() is the probability that link K is fully
occupied, conditional on
is the probability that link K is fully
occupied, conditional on ![]() (
( ![]() is also the probability that
link 3 is fully occupied, conditional on
is also the probability that
link 3 is fully occupied, conditional on ![]() ), so that
), so that
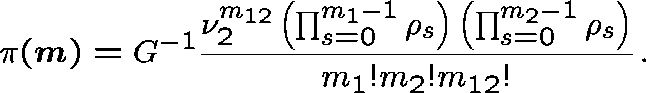
Once ![]() is estimated and
is estimated and ![]() determined, we set
determined, we set
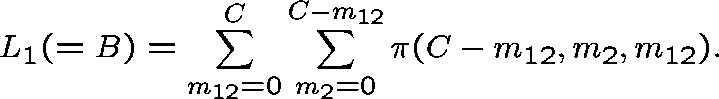
Similarly, ![]() can be expressed in terms of
can be expressed in terms of ![]() .
.
An estimate of ![]() can be found by assuming (incorrectly) that
can be found by assuming (incorrectly) that ![]() does not depend on
does not depend on ![]() . For
. For ![]() , set
, set
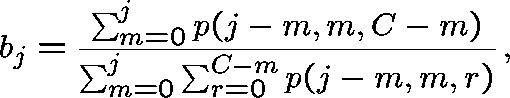
where
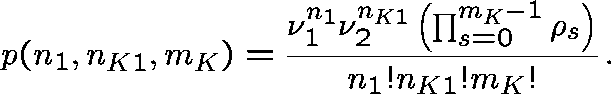
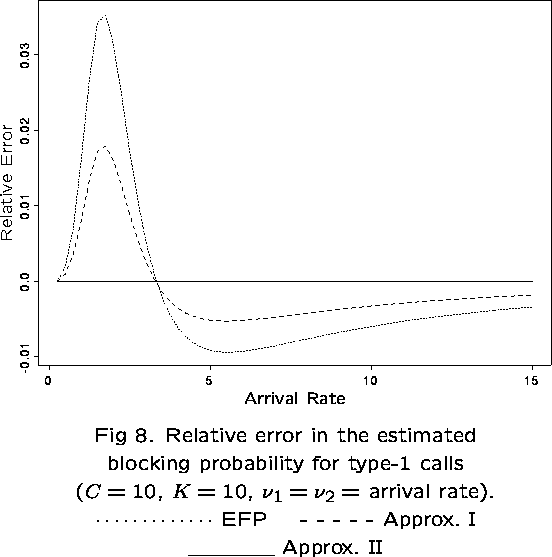
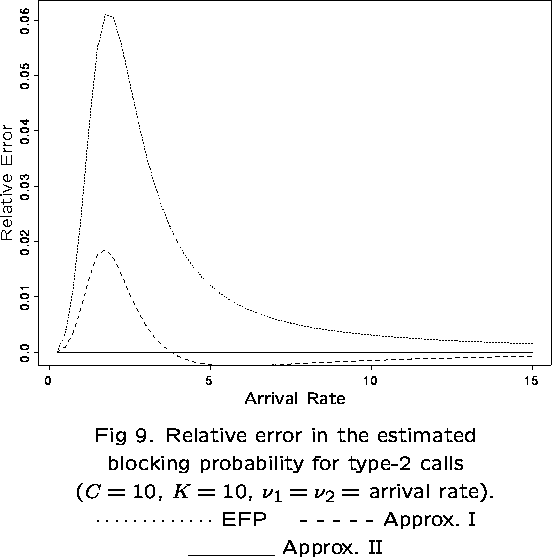
The dependence of ![]() on
on ![]() is due to the cyclic nature
of the network, but is expected to be slight for large networks. The
approximation is exact for the infinite line network, as
Zachary (1985) shows for a network which is equivalent to the one
considered here, with
is due to the cyclic nature
of the network, but is expected to be slight for large networks. The
approximation is exact for the infinite line network, as
Zachary (1985) shows for a network which is equivalent to the one
considered here, with ![]() (no single-link traffic). The
expression for
(no single-link traffic). The
expression for ![]() given above is equivalent to that obtained in his
paper for the infinite line network, although written in a different
form.
given above is equivalent to that obtained in his
paper for the infinite line network, although written in a different
form.
State-dependent arrival rates such as we have here are also discussed by various authors (for example, Pallant and Taylor (1994)). Kelly (1985) gives an exact expression in a line network (including some asymmetric cases).