WHAT ARE WE MODELLING?

Populations which are subject to crashes. Dramatic losses can occur due to

-

disease (eg a new virus)

-

food shortages (eg overbrowsing)

-

significant changes in climate.

Quasistationary behaviour. Such populations can survive for long periods before extinction occurs and can settle down to an apparently stationary regime.

Our goal. We seek to model this behaviour in order to properly manage these populations: to predict persistence times and to estimate population size.

Our model. The birth-death and catastrophe process predicts eventual extinction, but the time till extinction can be very long. The stationarity exhibited by these populations over any reasonable time scale can be explained using a quasistationary distribution.

THE MODEL

We use a continuous-time Markov process , where X(t) is the population size at time t, with transition rates given by

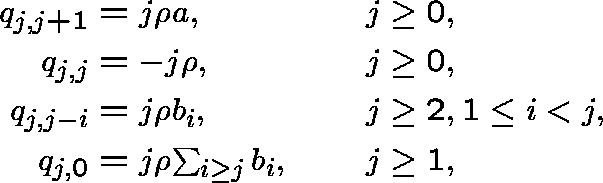
with the other transition rates equal to 0. Here, , a>0, for at least one i in , and .

Interpretation. For , is the instantaneous rate at which the population size changes from j to k, is the per capita rate of change and, given a change occurs, a is the probability that this results in a birth and  is the probability that this results in a catastrophe of size i (corresponding to the death or emigration of individuals).

SOME PROPERTIES

The state space. Clearly 0 is an absorbing state (corresponding to population extinction) and C is an irreducible class.

Extinction probabilities. If is the probability of extinction starting with i individuals, then for all if and only if D (the expected increment size), given by

is less than 0 (the subcritical case) or equal to 0 (the critical case).

In the supercritical case (D>0), the extinction probabilities can be expressed in terms of the probability generating function (pgf)

We find that

where b(s)=f(s)-s.

QUASISTATIONARY DISTRIBUTIONS

In order to describe the long-term behaviour of the process, we shall use two types of quasistationary distribution (QSD), called Type I and Type II, corresponding to the limits:

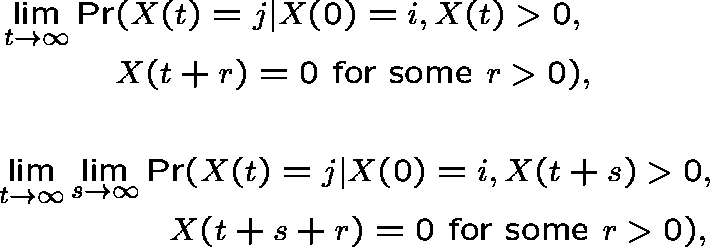
where . Thus, we seek the limiting probability that the population size is j, given that extinction has not occurred, or (in the second case) will not occur in the distant future, but that eventually it will occur; we have conditioned on eventual extinction to deal with the supercritical case, where this event has probability less than 1.

THE EXISTENCE OF QSDS

Consider the two eigenvector equations

where and C is the irreducible class.

In order that both QSDs exist, it is necessary that these equations have strictly positive solutions for some , these being the positive left and right eigenvectors of  (the transition-rate matrix restricted to C) corresponding to a strictly negative eigenvalue  .

Let be the maximum value of  for which positive eigenvectors exist ( is known to be finite), and denote the corresponding eigenvectors by and .

THE EXISTENCE OF QSDS

Proposition 5.1 of [1] can be restated for our purposes as follows (all sums are over k in C):

Proposition 1. Suppose that Q is regular.

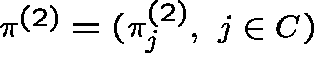(i) If converges, and either converges or is bounded, then the Type II QSD exists and defines a proper probability distribution over C, given by

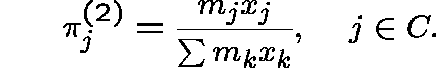
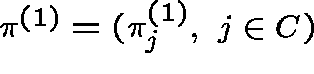(ii) If in addition converges, then the Type I QSD exists and defines a proper probability distribution over C, given by

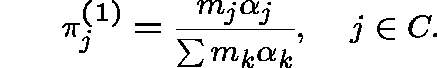
GEOMETRIC CATASTROPHES

We first examine the important special case 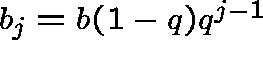, , where b>0, 0<q<1 and a + b = 1. Thus, given a jump occurs, it is a birth with probability a or a catastrophe with probability b, and the size of the catastrophe is determined by a geometric distribution.

We need to solve the right and left eigenvector equations. These are, respectively, for ,

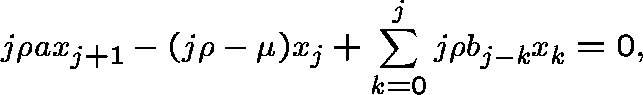
and, for ,

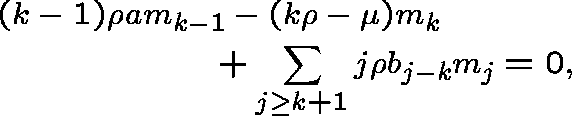
with the understanding that .

GEOMETRIC CATASTROPHES

We find that D = a - b/(1 - q), and that the maximum value of for which there exist strictly positive left and right eigenvectors is

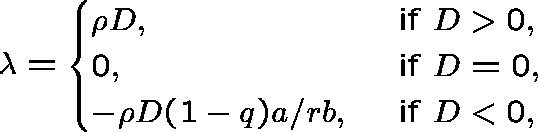
where r=a/(b+qa).

We deduce immediately that no QSD exists in the critical case (D=0). However, in both the supercritical (D>0) and subcritical (D<0) cases, both the Type I and the Type II QSDs exist.

GEOMETRIC CATASTROPHES

Supercritical case. When D>0 we find that 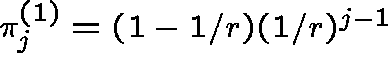(note that r>1 since D>0) and

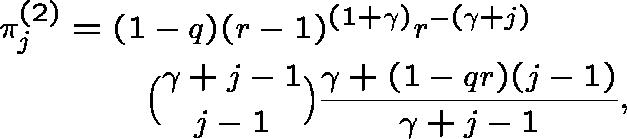
where ; note that .

Subcritical case. When D<0 we 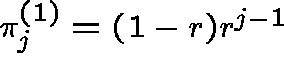find that , where as above r=a/(b+qa), but now r<1 since D<0. We also find that

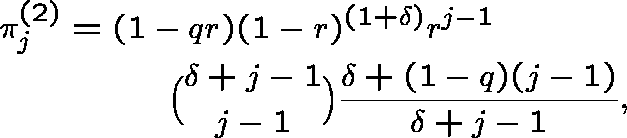
where ; note that .

THE GENERAL CASE

Recall that b(s)=f(s)-s, where f is the pgf given by 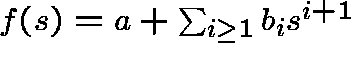, and D=-b'(1-). Recall also that, in the supercritical case, the absorption probabilities have generating function

( for all in the subcritical case). We will use the fact that b(s)=0 has a unique solution  on [0,1], and that or according as or D<0.

Lemma 1. .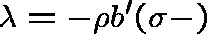

Theorem 1. In the subcritical case both types of QSD exist. The Type I QSD is given by 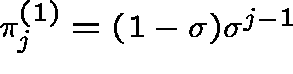(nice!), and the Type II QSD has pgf 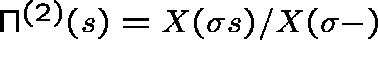, where

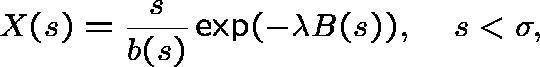
and, for , .

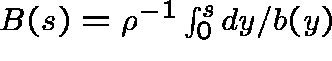THE GENERAL CASE

The supercritical case is more delicate. We require two extra conditions:

Condition (A). The catastrophe-size distribution has finite second moment, that is, 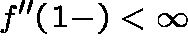(equivalently ).

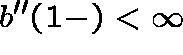Condition (B). The function b can be written

where L is slowly varying, that is, for large t.

Theorem 2. In the supercritical case both types of QSD exist under (A) and (B). The Type I QSD is given by 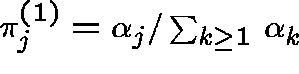, and the Type II QSD has pgf 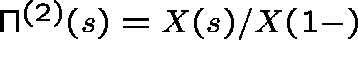, where

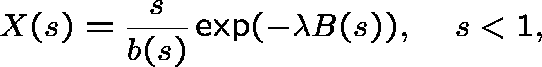
and, for s<1, 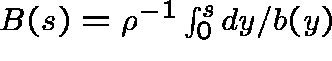.