Invited talk
for
Workshop celebrating Tony Pakes' 60th Birthday
by
Phil Pollett
The University of Queensland
ERGODICITY AND RECURRENCE
Pakes, A.G. (1969) Some conditions for ergodicity and recurrence of Markov chains. Operat. Res. 17, 1058-1061.
Let 
be an irreducible aperiodic Markov chain
taking values in the non-negative integers
and let
Then, 
for
all i sufficiently large is enough to guarantee recurrence, while
and 
is
sufficient for ergodicity.
This result has been used by many authors in a variety of contexts, for example, in the control of random access broadcast channels: slotted Aloha and CSMA/CD (Carrier sense multiple access with collision detect) protocol.
The Aloha Scheme
The following description is based on (Kelly, 1985)
.
Several stations use the same channel (assume infinitely many stations).
Packets arrive for transmission as a Poisson stream with rate 
(<1).
Time is broken down into ``slots" (0,1], (1,2], 
.
Let 
be the number of packets to arrive in the
slot (t-1,t] ( 
).
Their transmission will first be attempted
in the next slot (t,t+1].
Let 
represent the output of the channel at time t:
If 
, a ``collision'' has occurred, and retransmission will
be attempted in later slots,
independently in each slot with probability f until successful.
Thus, the transmission delay (measured in slots) has a geometric
distribution with parameter 1-f.
The backlog 
is a Markov chain with
Thus,
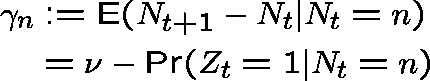
and
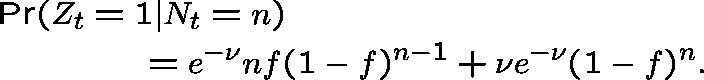
We deduce that 
for all n sufficiently large.
Indeed the chain is transient
(Kleinrock (1983), Fayolle, Gelenbe and Labetoulle (1977),
Rosenkrantz and Towsley (1983)).
State-dependent Retransmission
Now suppose that the retransmission probability is allowed to depend
on the backlog: 
when 
.
Then, 
is maximized by
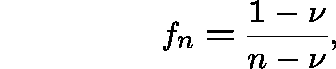
and, with this choice,
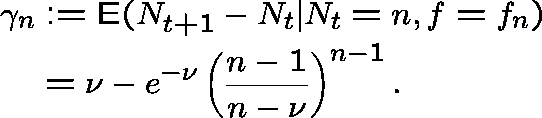
Thus, 
and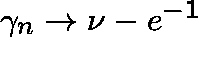 
. Thus,
is ergodic, that is, the backlog is eventually cleared, if
.
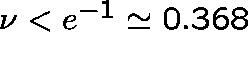But, users of the channel do not know the backlog, and thus cannot determine the optimal retransmission probability.
Towards a Better Control Scheme
It would be better to choose the
retransmission probability 
based on the observed channel output.
Several schemes have been suggested by Mikhailov (1979) and
Hajek and van Loon (1982).
For example, suppose each station maintains a counter 
,
updated as follows: 
and
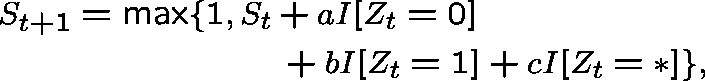
where a,b and c are to be specified.
For example, (a,b,c) = (-1,0,1) is an obvious choice.
Suppose that 
.
Then, 
is a Markov chain.
We would like to ``track'' the backlog, at least when 
is large.
Consider the drift in 
:
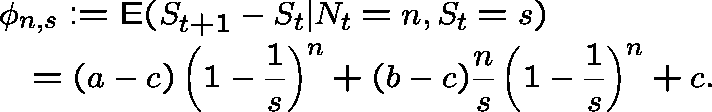
Let 
with 
held fixed. Then,
The choice 
, where 
,
makes the drift in
negative if 
and
positive if 
.
Thus, if the backlog were held steady at a large value, then the counter
would approach that value. Also,
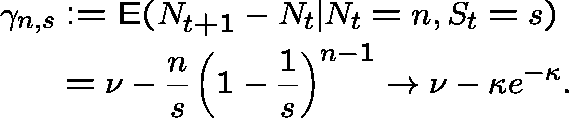
Mikhailov (1979) showed that the choice
(a,b,c) =(2-e,0,1) ensures that
is ergodic whenever 
.
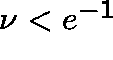Question. For an irreducible aperiodic Markov chain ,
can one infer anything about its ergodicity and recurrence from the
marginal drifts?
THE BIRTH-DEATH AND CATASTROPHE PROCESS
Pakes, A.G. (1987) Limit theorems for the population size of a birth and death process allowing catastrophes. J. Math. Biol. 25, 307-325.
An appropriate model for populations that are subject to crashes (dramatic losses can occur in animal populations due to disease, food shortages, significant changes in climate).
Such populations can exhibit quasi-stationary behaviour: they may survive for long periods before extinction occurs and can settle down to an apparently stationary regime. This behaviour can be modelled using a limiting conditional (or quasi-stationary) distribution.
The Model
It is a continuous-time Markov chain
, where X(t) represents the
population size at time t, with transition
rates 
given by
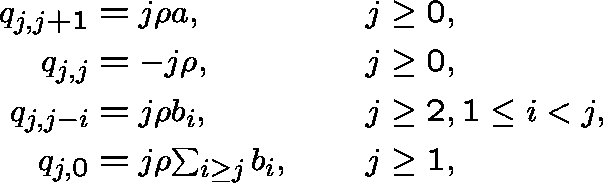
with the other transition rates equal to 0. Here, 
, a>0 and 
for at least one i in 
, and, 
.
Interpretation.
For 
, 
is the instantaneous rate at which the population
size changes from j to k, 
is the per capita rate of change
and, given a change occurs, a is the probability that this results in
a birth and 
is the probability that this results in a catastrophe
of size i (corresponding to the death or emigration of i individuals).
Some Properties
The state space. Clearly 0 is an absorbing state (corresponding to population extinction) and C is an irreducible class.
Extinction probabilities.
If 
is the probability of extinction
starting with i individuals, then 
for all 
if and only if D (the expected increment size), given by
is less than 0 (the subcritical case) or equal to 0 (the critical case).
In the supercritical case (D>0), the extinction probabilities can be expressed in terms of the probability generating function
We find that
where b(s)=f(s)-s.
Limiting Conditional Distributions
In order to describe the long-term behaviour of the process, we use two types of limiting conditional distribution (LCD), called Type I and Type II, corresponding to the limits:
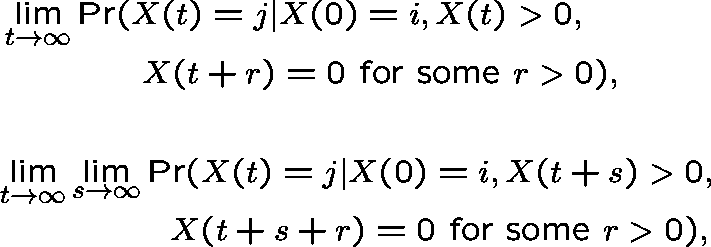
where 
. Thus, we seek the limiting probability that the
population size is j, given that extinction has not occurred, or (in
the second case) will not occur in the distant future, but that
eventually it will occur; we have conditioned on eventual extinction
to deal with the supercritical case, where this event has probability
less than 1.
The Existence of Limiting Conditional Distributions
Consider the two eigenvector equations
where 
and C is the irreducible class.
In order that both types of LCD exist, it is necessary that these
equations have strictly positive solutions for some 
, these being
the positive left and right eigenvectors of 
(the transition-rate
matrix restricted to C) corresponding to a strictly negative
eigenvalue 
.
Let 
be the maximum value of 
for which
positive eigenvectors exist ( is known to be finite), and denote
the corresponding eigenvectors by 
and 
.
The Existence of Limiting Conditional Distributions
Proposition. Suppose that Q is regular.
converges, and either 
converges or 
is bounded, then the Type II LCD exists and defines a proper probability
distribution 
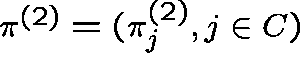over C, given by
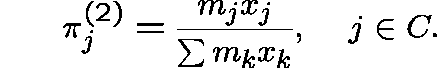
(All unmarked sums are over k in C.)
converges, then the Type I LCD exists
and defines a proper probability distribution 
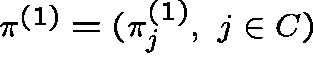over C, given by
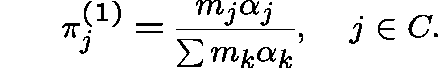
Try to use PKP Technology
We need the fact that b(s)=0 has a unique solution 
on [0,1],
and that 
or 
according as 
or D<0.
Setting 
,
the eigenvector equations can be written (for 
) as
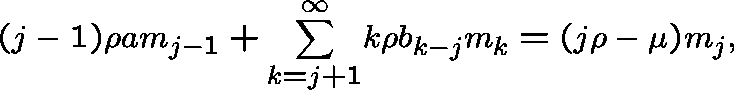
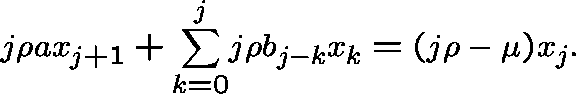
What is the maximum value of for which a positive solution exists?
If is any solution to the second, then its
generating function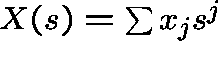 
satisfies
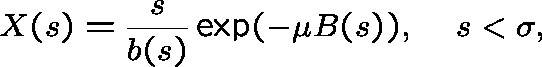
where, for 
, 
.
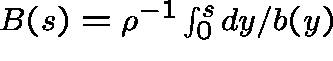Using this approach, we cannot really avoid the question: when
is X(s) a power series with non-negative coefficients?
The function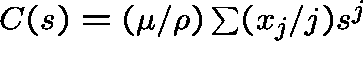 
satisfies
So, equivalently, we ask: when does C(s) have non-negative coefficients?
This is answered in the following paper (assuming, as we have here, that B(s) is a power series with non-negative coefficients):
Pakes, A.G. (1997) On the recognition and structure of probability generating functions. In (Eds. K.B. Athreya and P. Jagers) Classical and Modern Branching Processes, IMA Vols. Math. Appl. 84, Springer, New York, pp. 263-284.
Lemon. The maximum value of
for which a positive right eigenvector exists is
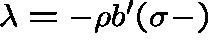. When 
, the
left eigenvector is given by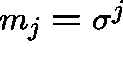 
, .
The Subcritical Case
We have D:=-b'(1-)<0 and 
.
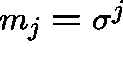Since , , we have also
and 
.
The combination of technologies thus yields:
Theorem. In the subcritical case both types of LCD exist. The Type I LCD is given by
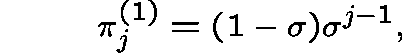
and the Type II LCD has pgf
where
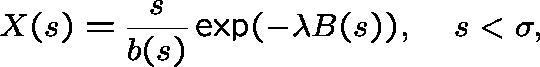
and, for , .
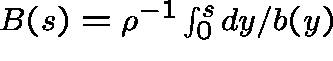This result is contained in Theorems 5.1 and 6.2 of Pakes (1987).
The Supercritical Case
We have D>0 and , and
the absorption probabilities have generating function
Since 
, , we have
and 
. When do these series converge?
Condition (A). The catastrophe-size distribution has
finite second moment, that is,
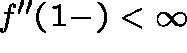(equivalently 
).
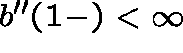Condition (B). The function b can be written
where L is slowly varying, that is,
for large t.
Theorem. In the supercritical case,
the Type I LCD exists under (A), and is given by
.
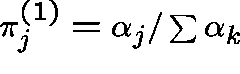If in addition (B) holds, then the Type II LCD exists and has
pgf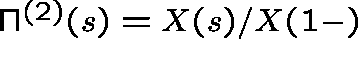 
.
This first part (Type I LCD) is contained in:
Pakes, A.G. and Pollett, P.K. (1989) The supercritical birth, death and catastrophe process: limit theorems on the set of extinction. Stochastic Process. Appl. 32, 161-170.
The second part (Type II LCD) is contained in Theorem 6.2 of Pakes (1987).
Other papers important to my work:
Pakes, A.G. (1971) A branching process with a state dependent immigration component. Adv. Appl. Probab. 3, 301-314.
Pakes, A.G. (1975) On the tails of waiting-time distributions. J. Appl. Probab. 12, 555-564.
Pakes, A.G. (1992) Divergence rates for explosive birth processes. Stochastic Process. Appl. 41, 91-99.
Pakes, A.G. (1993) Explosive Markov branching processes: entrance laws and limiting behaviour. Adv. Appl. Probab. 25, 737-756.
Pakes, A.G. (1993) Absorbing Markov and branching processes with instantaneous resurrection. Stochastic Process. Appl. 48, 85-106.
Pakes, A.G. (1995) Quasi-stationary laws for Markov processes: examples of an always proximate absorbing state. Adv. Appl. Probab. 27, 120-145.
