Identifying Q-processes with a given finite m-invariant measure
by
Phil Pollett

Department of Mathematics
The University of Queensland
Identifying Q-processes with a given finite m-invariant measure
by
Phil Pollett

Department of Mathematics
The University of Queensland
PRELIMINARIES
State-space: ![]()
Transition functions:
A set of real-valued functions ![]() ,
, ![]() defined on
defined on ![]() is called a process
(or transition function) if
is called a process
(or transition function) if
It is called standard
and honest if
for some (and then for all) t>0.
THE Q-MATRIX
For a standard process P the right-hand derivative
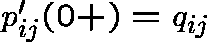 exists and defines a q-matrix
exists and defines a q-matrix
![]() whose entries satisfy
whose entries satisfy
We set ![]() ,
, ![]() .
.
Suppose that Q is given.
Assume that Q is stable, that is ![]() for all i in S.
A standard process P will then be called a Q-process
if its q-matrix is Q.
for all i in S.
A standard process P will then be called a Q-process
if its q-matrix is Q.
THE KOLMOGOROV DIFFERENTIAL EQUATIONS
For simplicity, we shall assume that Q is conservative, that is
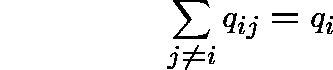
for all ![]() .
Under this condition, every Q-process P
satisfies the backward equations,
.
Under this condition, every Q-process P
satisfies the backward equations,
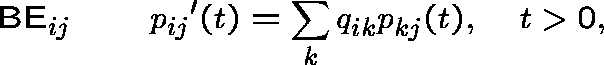
but might not satisfy the forward equations,
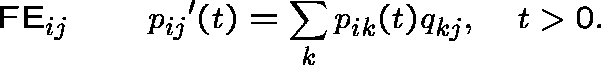
STATIONARY DISTRIBUTIONS
A collection of positive numbers ![]() is a
stationary distribution if
is a
stationary distribution if
![]() and
and
Recipe: Find a collection of strictly positive numbers
![]() such that
such that
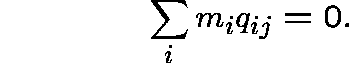
Such an m is called an invariant measure for Q.
If ![]() , then we set
, then we set
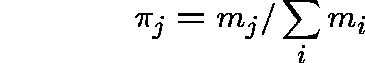
and hope that ![]() satisfies (2).
satisfies (2).
BIRTH-DEATH PROCESSES
Transition rates:
![]() (
( ![]() - birth rates)
- birth rates)
![]() (
( ![]() - death rates) (
- death rates) ( ![]() )
)
Solve:
![]() ,
, ![]() , that is,
, that is,
![]()
and, for ![]() ,
,
![]()
Solution: ![]() and
and
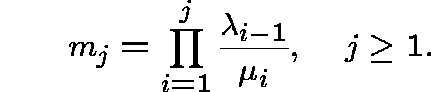
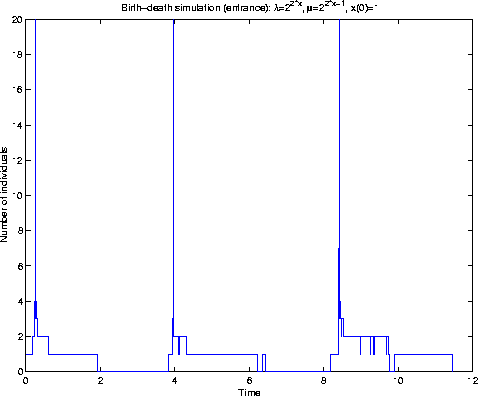
MILLER'S EXAMPLE
Rates: fix r>0 and set
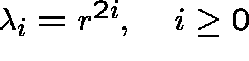 ,
,
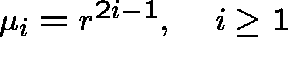 .
.
Solution: ![]() and
and
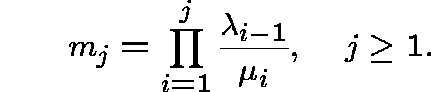
So,
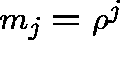 , where
, where ![]() ,
,
and hence if r>1,
![]()
[Download a postscript version of the above image]
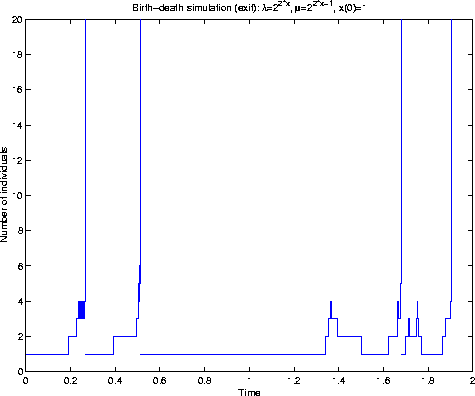
WHAT IS GOING WRONG?
Rates:
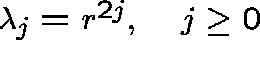 ,
,
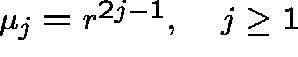 .
.
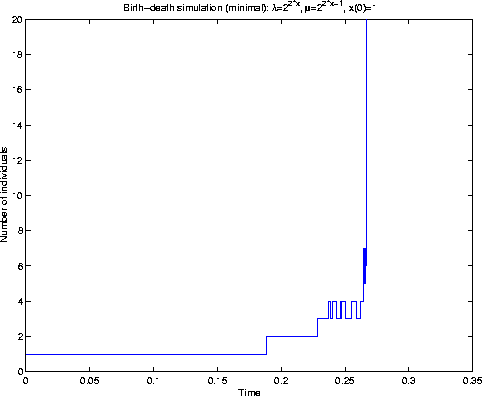
The relative proportion of births to deaths is r and so, if r>1, the ``process'' is clearly transient.
In fact, the ``process'' is explosive: Q is not regular.
R.G. Miller![]() showed that Q needs to be regular for the
recipe to work.
showed that Q needs to be regular for the
recipe to work.
THE MOTIVATING QUESTION
If Q is regular, then there exists uniquely a Q-process, namely the
minimal process: the minimal solution ![]() ,
, ![]() to BE.
to BE.
If Q is not regular there are infinitely many Q-processes, infinitely many of which are honest.
Question:
Suppose that there exists
a collection of strictly positive numbers
![]() such that
such that
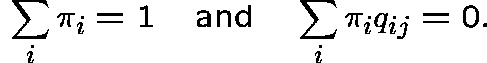
Does ![]() admit an interpretation as a stationary distribution for any of
these processes?
admit an interpretation as a stationary distribution for any of
these processes?
[Download a postscript version of the above image]
[Download a postscript version of the above image]
AN INVARIANCE RESULT
Let ![]() be a collection of strictly positive numbers.
We call m a subinvariant measure for Q if
be a collection of strictly positive numbers.
We call m a subinvariant measure for Q if
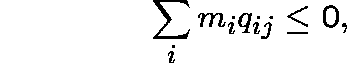
and an invariant measure for Q if
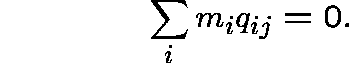
It is called an invariant measure for P if
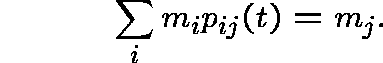
Theorem: Let P be an arbitrary Q-process. If m is invariant for P, then m is subinvariant for Q, and invariant for Q if and only if P satisfies the forward equations FE over S.
Corollary: If m is invariant for the minimal process F, then m is invariant for Q.
A CONSTRUCTION PROBLEM
Suppose that Q is a stable and conservative q-matrix, and that m is subinvariant for Q.
Problem 1: Does there exist a Q-process for which m is invariant?
Problem 2: Does there exist an honest Q-process for which m is invariant?
Problem 3: When such a Q-process exists, is it unique?
Problem 4: In the case of non-uniqueness, can one identify all Q-processes (or perhaps all honest Q-processes) for which m is invariant?
THE RESOLVENT
Let P be a transition function. If we write
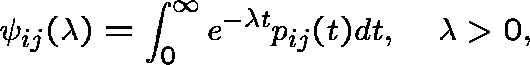
for the Laplace transform of ![]() , then
, then
![]() enjoys the following
(analogous) properties:
enjoys the following
(analogous) properties:
![]() is called the resolvent of P. Indeed, if
is called the resolvent of P. Indeed, if
![]() is a given resolvent, in that it satisfies these properties, then
there exists a standard (!) process P
with
is a given resolvent, in that it satisfies these properties, then
there exists a standard (!) process P
with ![]() as its resolvent
as its resolvent![]() .
.
IDENTIFYING Q-PROCESSES USING RESOLVENTS
Now, if one is given a stable and conservative q-matrix Q,
together with a resolvent ![]() which satisfies the backward equations,
which satisfies the backward equations,
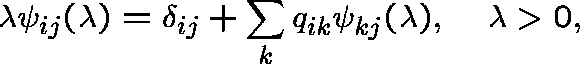
then ![]() determines a standard Q-process. In particular,
as
determines a standard Q-process. In particular,
as ![]() ,
,
One can also use the resolvent to determine whether or not the Q-process is honest, for this happens when and only when
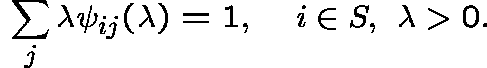
IDENTIFYING INVARIANT MEASURES USING RESOLVENTS
Theorem: Let P be an arbitrary process and let ![]() be its resolvent.
Then, m is invariant for P if and only if it is invariant for
be its resolvent.
Then, m is invariant for P if and only if it is invariant for ![]() ,
that is,
,
that is,
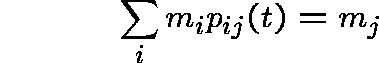
if and only if
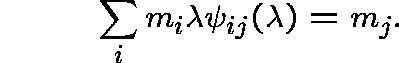
THE EXISTENCE OF A Q-PROCESS WITH A GIVEN INVARIANT MEASURE
Theorem:
Let Q be a stable and conservative q-matrix, and suppose that m
is a subinvariant measure for Q.
Let ![]() be the resolvent of
the minimal Q-process and define
be the resolvent of
the minimal Q-process and define ![]() and
and ![]() by
by
![]() ,
,
and
![]() .
.
Then, if d=0, m is invariant for the minimal Q-process. Otherwise, if
![]() ,
,
for all ![]() ,
there exists a Q-process P for which m is invariant.
,
there exists a Q-process P for which m is invariant.
THE EXISTENCE OF A Q-PROCESS WITH A GIVEN INVARIANT MEASURE
Theorem continued: The resolvent of one such process is given by
and this process is honest if and only if
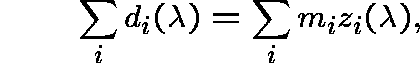
for all ![]() .
A sufficient condition for there to exist an honest Q-process for which m is
invariant is that m satisfies
.
A sufficient condition for there to exist an honest Q-process for which m is
invariant is that m satisfies
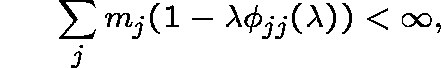
for all ![]() .
.
Corollary: If m is a subinvariant probability distribution for Q, then there exists an honest Q-process with stationary distribution m. The resolvent of one such process is given by (4).
THE SINGLE-EXIT CASE
Suppose that Q is a single-exit q-matrix,
that is, the space of bounded,
non-negative vectors ![]() which satisfy
which satisfy
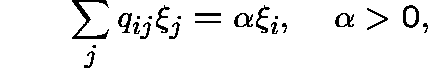
has dimension 1. (The minimal process has only one available ``escape route'' to infinity). Then, the condition
![]()
is necessary for the existence of a Q-process for which the specified measure is invariant; the Q-process is then determined uniquely by
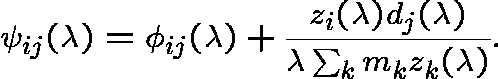
NON-UNIQUENESS
Consider a pure-birth process with strictly positive birth rates
![]() , but
imagine that we have two distinct sets of birth rates,
, but
imagine that we have two distinct sets of birth rates,
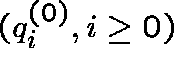 and
and 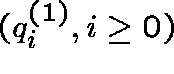 ,
which satisfy
,
which satisfy
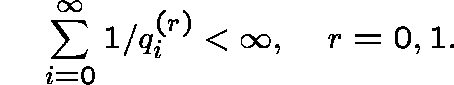
Let ![]() and define
and define
![]() by
by
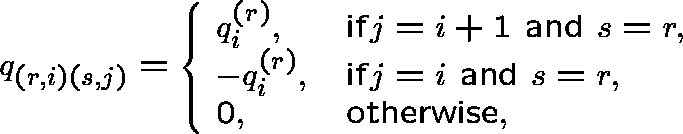
for r=0,1 and ![]() .
The measure
.
The measure ![]() , given by
, given by
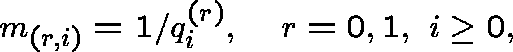
is subinvariant for Q.

NON-UNIQUENESS
The resolvents of two distinct Q-processes for which m is invariant are given by
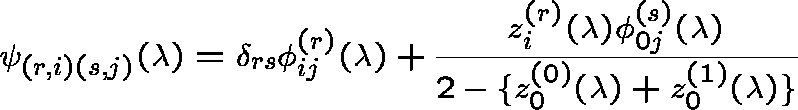
and
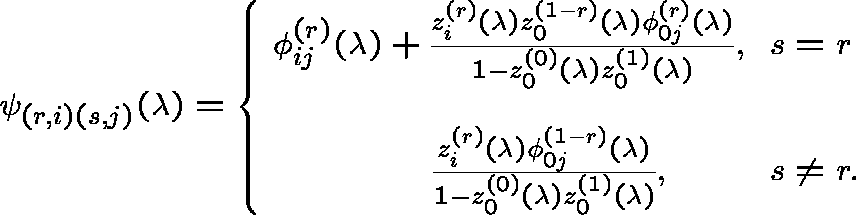
Interpretation: The first process chooses between (0,0) and (1,0) with equal probability as the starting point following an explosion, no matter which was the most recently traversed path, and the second process traverses alternate paths following successive explosions.
THE REVERSIBLE CASE
Suppose that Q is symmetrically reversible with respect to m,
that is, ![]() ,
, ![]() .
Then,
.
Then, ![]() , and so we
arrive at the following corollary due to Hou and Chen
, and so we
arrive at the following corollary due to Hou and Chen![]() .
.
Corollary:
If Q is reversible with respect to m, then there exists uniquely
a Q-function P for which m is invariant if and only if
![]() , for all
, for all ![]() . It is honest and
its resolvent is given by
. It is honest and
its resolvent is given by
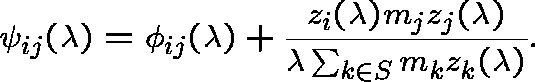
Moreover, P is reversible with respect to m in that
![]() (or, equivalently,
(or, equivalently,
![]()
![]() ).
).
BIRTH-DEATH PROCESSES
Suppose that the birth rates ![]() and death rates
and death rates ![]() are strictly positive.
The q-matrix Q is then regular if and only if
are strictly positive.
The q-matrix Q is then regular if and only if
Proposition:
Let ![]() be the
essentially unique invariant measure for Q.
be the
essentially unique invariant measure for Q.
(i) m is invariant for the minimal Q-process if and only if (6) holds.
(ii) When (6) fails, there exists uniquely a Q-process P for which m is invariant if and only if m is finite, in which case P is the unique, honest Q-process which satisfies FE; P is positive recurrent and its stationary distribution is obtained by normalizing m.
![]() -INVARIANCE
-INVARIANCE
Suppose that ![]() , where 0 is an absorbing state and C is
irreducible (for F). Let
, where 0 is an absorbing state and C is
irreducible (for F). Let ![]() .
A collection
.
A collection ![]() of strictly positive numbers
is called a
of strictly positive numbers
is called a ![]() -subinvariant measure for Q if
-subinvariant measure for Q if
![]()
and a ![]() -invariant measure for Q if
-invariant measure for Q if
![]()
It is called a ![]() -invariant measure for P, where P
is any transition function, if
-invariant measure for P, where P
is any transition function, if
![]()
Proposition:
A probability distribution ![]() is a
is a ![]() -invariant measure
for some
-invariant measure
for some ![]() if and only if it is a quasistationary distribution: for
if and only if it is a quasistationary distribution: for ![]() ,
,
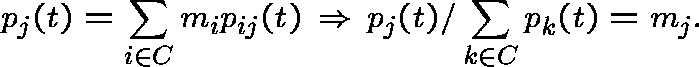
![]() -INVARIANCE FOR F
-INVARIANCE FOR F
Theorem:
If m is ![]() -invariant for P, then m is
-invariant for P, then m is ![]() -subinvariant for Q, and
-subinvariant for Q, and
![]() -invariant for Q if and only if P satisfies the
forward equations over C.
For example, if m is
-invariant for Q if and only if P satisfies the
forward equations over C.
For example, if m is ![]() -invariant for the minimal process,
then it is
-invariant for the minimal process,
then it is ![]() -invariant for Q.
-invariant for Q.
Theorem:
If m is ![]() -invariant for Q, then it is
-invariant for Q, then it is ![]() -invariant for F if and only if the equations
-invariant for F if and only if the equations
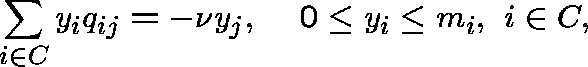
have no non-trivial solution for some (and then all) ![]() .
.
Theorem:
If m is a finite
![]() -invariant measure for Q, then
-invariant measure for Q, then
where 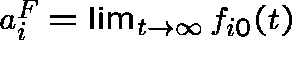 , and m
is
, and m
is ![]() -invariant for F if and only if equality holds in (8).
-invariant for F if and only if equality holds in (8).
Q-PROCESSES WITH A GIVEN
![]() -INVARIANT MEASURE
-INVARIANT MEASURE
Theorem:
Suppose that Q is single-exit
and that m is a finite ![]() -subinvariant measure for Q.
Then, there exists a Q-process for which m is
-subinvariant measure for Q.
Then, there exists a Q-process for which m is ![]() -invariant
if and only if
-invariant
if and only if
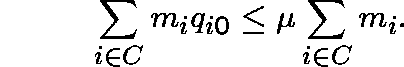
The resolvent ![]() of any Q-process for which m is
of any Q-process for which m is ![]() -invariant must be of the form
-invariant must be of the form
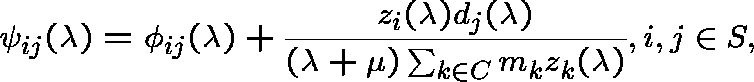
where
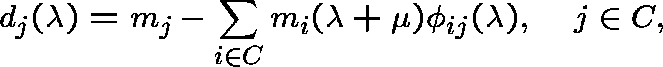
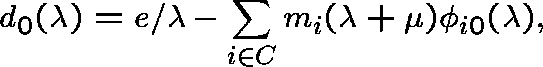
and e satisfies
![]() .
.
Q-PROCESSES WITH A GIVEN
![]() -INVARIANT MEASURE
-INVARIANT MEASURE
Theorem continued: Conversely, if
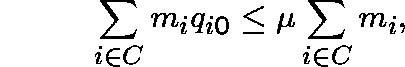
then all Q-processes for which m is ![]() -invariant
can be constructed in this way by varying e in the
range
-invariant
can be constructed in this way by varying e in the
range
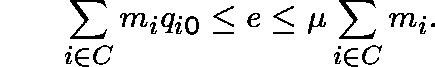
Exactly one of these is honest; this is obtained by setting ![]() . And, exactly one satisfies the forward equations
FE
. And, exactly one satisfies the forward equations
FE ![]() over
over ![]() ; this is obtained by setting
; this is obtained by setting ![]() .
.