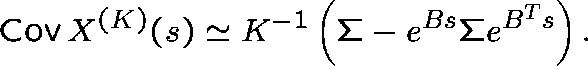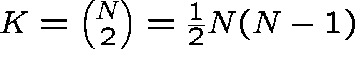MODELLING BISTABILITY IN TELECOMMUNICATIONS NETWORKS

by

Phil Pollett

Department of Mathematics
The University of Queensland

A SYMMETRIC FULLY-CONNECTED NETWORK

N - nodes

- links

C - circuits on each link

Poisson traffic offered at rate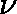

Exponentially distributed holding times (mean 1)

THE GHK MODEL

Let 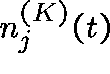be the number of links with j circuits in use at time t (for a network with K links).

Let 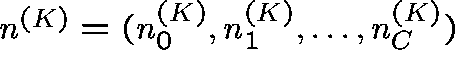. Then, 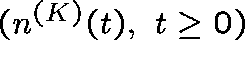is a continuous-time Markov chain which takes values in

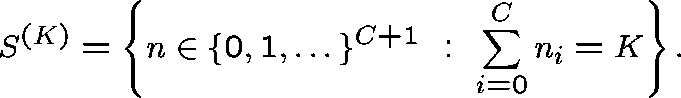
The transition rates, 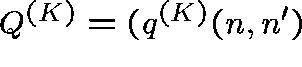, , 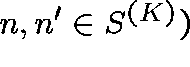of the process are given by

,

,

,

,

,

,

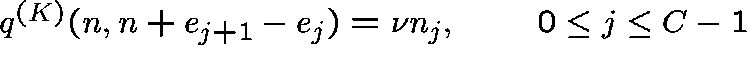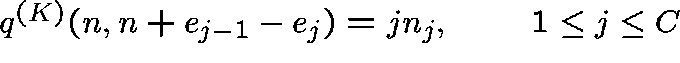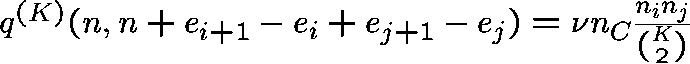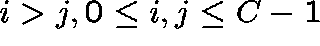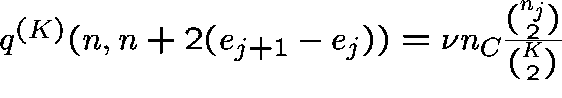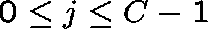where 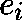is the unit vector with 1 as its 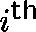entry.

THE BEHAVIOUR AS THE NETWORK BECOMES LARGE

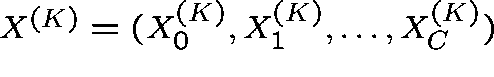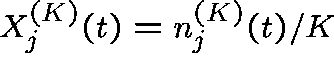Let , where is the proportion of links with j circuits in use at time t.

If, as , , 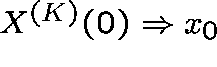then 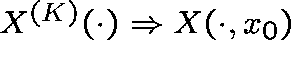, where 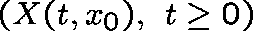is a deterministic process with initial point 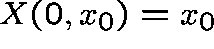and which satisfies ,

,

,

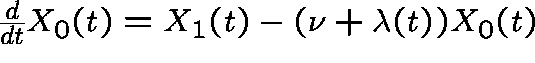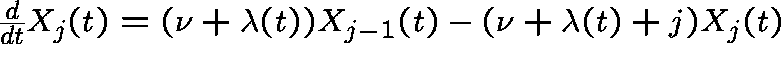
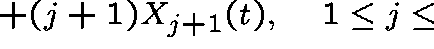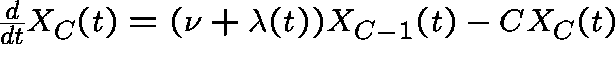where .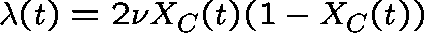

THE EQUILIBRIUM POINTS

If 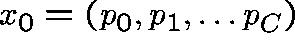is an equilibrium point it must be of the form given by

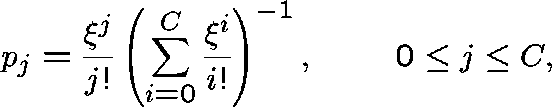
where 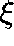solves

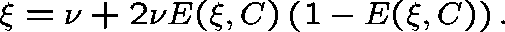
The quantity 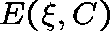, given by

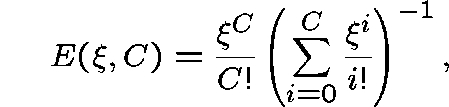
is Erlang's formula for the loss probability of a single link with C circuits and with Poisson traffic offered at rate 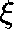. It is usually more convenient to calculate the equilibrium points by setting 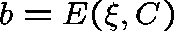and solving the equation

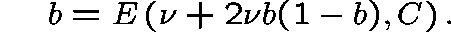
MODELLING RANDOM FLUCTUATIONS

The central limit law shows that the random fluctuations about any given equilibrium point, 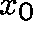, are Gaussian. Moreover, it shows that these fluctuations can be approximated by an Ornstein-Uhlenbeck (OU) process.

Let 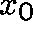be an equilibrium point. Then, if

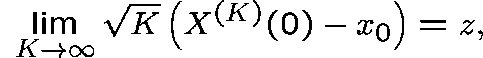
the family of processes 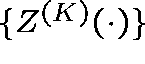, defined by

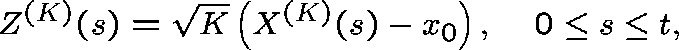
converges weakly to an Ornstein-Uhlenbeck process with initial value 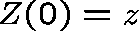and with a local drift matrix, B, and a local covariance matrix, G, which can be determined from the parameters of the model.

In particular, 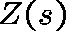is normally distributed with mean

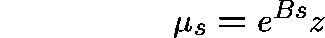
and covariance matrix

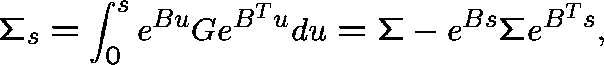
where , the stationary covariance matrix, satisfies

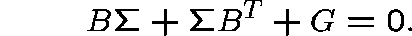
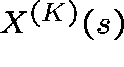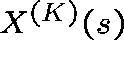We can conclude that, for K large, has an approximate normal distribution for each s, and an approximation for the mean and the covariance matrix of is given by

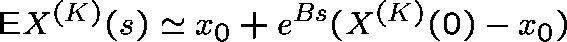
and