A RANDOM GRAPH

The construction. A random (undirected) graph with n vertices is constructed in the following way: pairs of vertices are selected one at a time in such a way that each pair has the same probability of being selected on any given occasion, and, each selection is made independently of previous selections. If the vertex pair is selected, then an edge is constructed which connects x and y.

Are multiple edges possible? In my model, yes! For example, if the vertex pair were to be selected k times, there would be k edges connecting x and y: a multiple edge contributing cycles of length 2.

ASYMPTOTIC BEHAVIOUR

Suppose that m edges have been selected. We shall be concerned with the behaviour of the graph in the limit as n and m become large, but in such a way that m=O(n).

The problem. Our problem is to determine the limiting probability that the graph is acyclic.

Motivation. Havas and Majewski present an algorithm for minimal perfect hashing (used for memory-efficient storage and fast retrieval of items from static sets) based on this random graph. Their algorithm is optimal when the graph is acyclic.

WHY ACYCLIC?

Consider a set W of m words (or keys). Every bijection , where , is called a minimal perfect hash function. HM find hash functions of the form

map keys to integers (they identify the pair of vertices of the graph corresponding to the edge w) and g maps integers to I.

Given and , can g be chosen so that h is a bijection?

If the graph is acyclic then, yes, it is easy to construct g from h. Traverse the graph: if vertex w is reached from vertex u then set

where e=(u,w).

EFFICIENCY

HM's algorithm generates and at random until an acyclic graph is found:

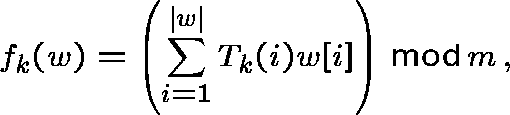
where and are tables of random integers and w[i] denotes the i-th character (an integer) of key i.

The efficiency of the algorithm is determined by the probability 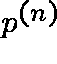that the graph is acyclic: the expected number of iterations needed to find an acyclic graph will be 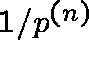(typically between 2 and 3).

EVALUATING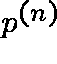

Theorem. If n and m tend to in such a way that , where c is a positive constant, the limiting probability p that the graph is acyclic is given by

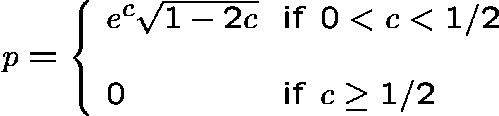
Proof. On request. It uses results from [HM] and Erdös and Renyi.

SKETCH PROOF

Let 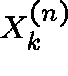be the number of cycles of length k and let 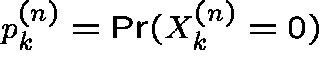. Following [HM] write

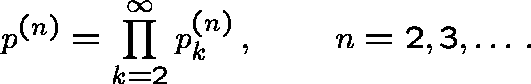
Now let 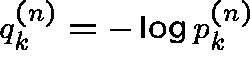, so that 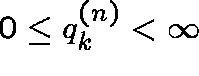and

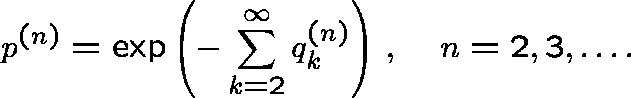
ER show that the distribution of 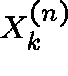is asymptotically Poisson: in particular,

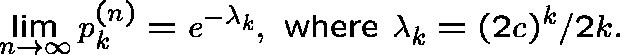
It follows that

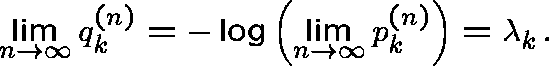
So, formally,

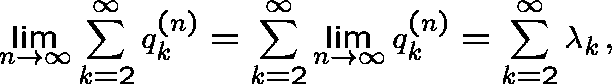
and hence

By Fatou's Lemma, we always have

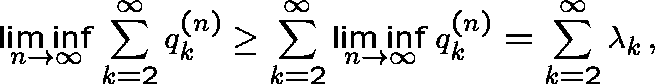
from which it follows immediately that

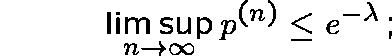
this argument is valid even if the sum in (2) is divergent. We deduce immediately that if , .

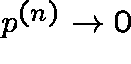When c<1/2, we have and

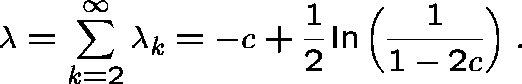
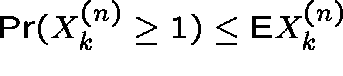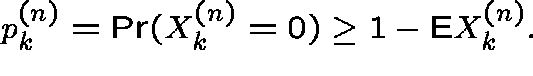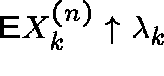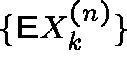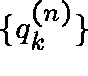From Markov's inequality we have and so By Lemma 2 of [HM], we have, for each fixed , that as . In particular, for each , the sequence is bounded above by . It follows that is bounded above by . Further, since ,

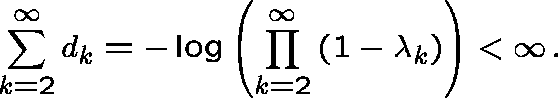
Thus, by Dominated Convergence, we have

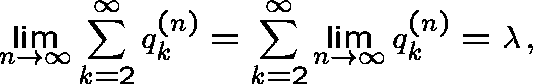
and, hence, .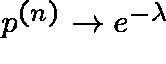

THE FIVE STAGES OF EVOLUTION

PRIMORDIAL STEW: m(n)=o(n)

If , then (with limiting probability 1) all components are trees.

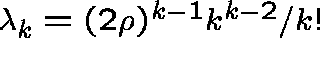Trees of order k appear when m reaches order . In particular, , the number of trees of order k, has a (limiting) Poisson distribution with mean , where

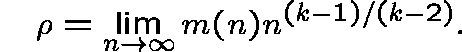
Finally, if 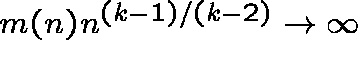, the number of trees of order k is asymptotically normally distributed with mean and variance equal to

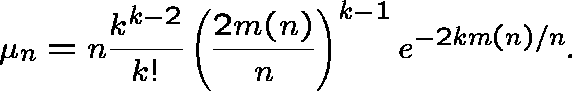
To be precise, 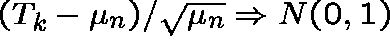. This result holds in the next two stages of evolution; we only require .

SPOOKY: , where 0<c<1/2

Cycles of all orders start to appear: , the number of cycles of order k, has a (limiting) Poisson distribution with mean .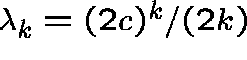

Furthermore, with limiting probability 1, all components are either trees or consist of exactly one cycle (k vertices and k edges), the latter having a Poisson distribution with mean

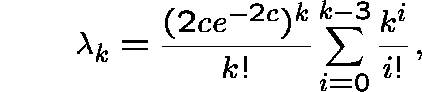
where k is the order of the cycle.

The largest component is a tree; it has

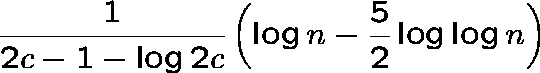
vertices (with probability tending to 1).

A MONSTER APPEARS: , where

When (c=1/2), the largest component has (with probability tending to 1) vertices. When with c>1/2, a giant component appears: the largest component in the graph has G(c) n vertices, where G(c)=1-X(c)/2c and

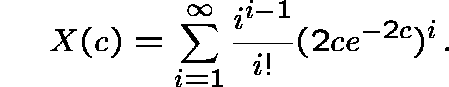
Note that G(1/2)=0 and as .

Almost all the other vertices belong to trees: the total number of vertices belonging to trees is almost surely n(1-G(c))+o(n).

For c>1/2, the expected number of components in the graph is asymptotically

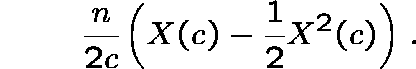
CONNECTEDNESS: , where

The graph is becoming connected: if

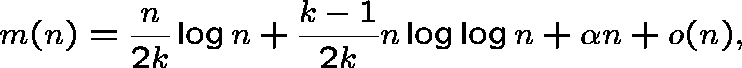
then (with probability tending to 1) there are only trees of order outside the giant component, the limiting distribution of the number of trees of order l being Poisson with mean 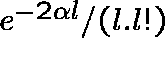. For example (k=1), if

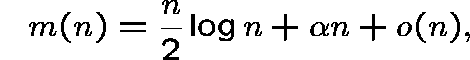
there are (almost surely) only isolated vertices outside the giant component, the number of these having a limiting Poisson distribution with mean . And, the chance that the graph is indeed connected tends to 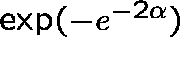(which itself tends to 1 as grows).

ASYMPTOTIC REGULARITY: , where

The whole graph becomes regular: with probability tending to 1, the graph becomes connected and the orders of all vertices are equal.