MODELLING QUASISTATIONARITY IN EVANESCENT PROCESSES
by
Phil Pollett
Department of Mathematics
The University of Queensland
(Download the following image (as postscript)):

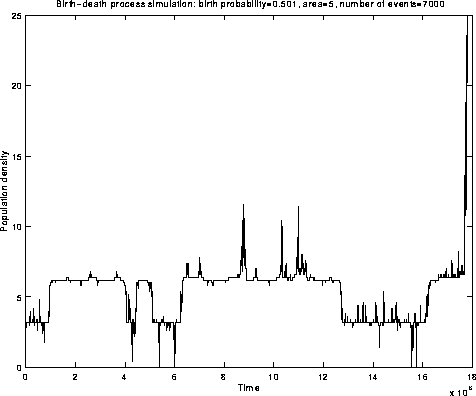
Figure 1. Quasistationarity of an explosive population process
[Simulation |
java code]
QUASISTATIONARITY
Processes appear to be stationary over any reasonable time scale, yet they are evanescent.
Examples:
AN AUTO-CATALYTIC REACTION
Consider the following reaction scheme:

where X is a catalyst. Suppose that there are two stages, namely
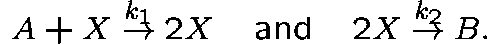
Let 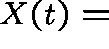 number of X molecules at time t.
number of X molecules at time t.
Suppose that the concentration of A is held constant;
let a be the number of molecules of A.
The state space is 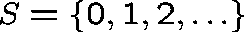 and the transition rates,
and the transition rates, 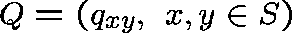 , are given by
, are given by
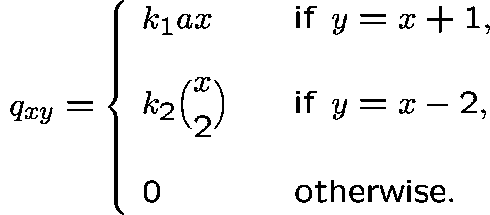
(Download the following image (as postscript)):
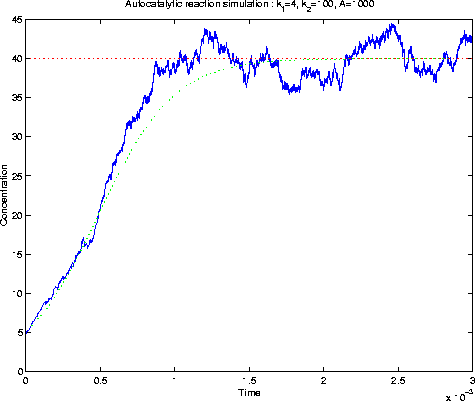
Figure 2. Auto-catalytic reaction simulation
[Simulation |
java code]
AN EPIDEMIC MODEL
(Ridler-Rowe)
The state at time t:
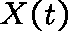 - number of susceptibles
- number of susceptibles
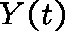 - number of infectives
- number of infectives
State space:
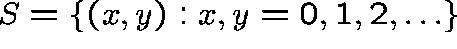
Transition rates 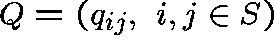 :
:
if 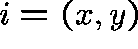 , then
, then
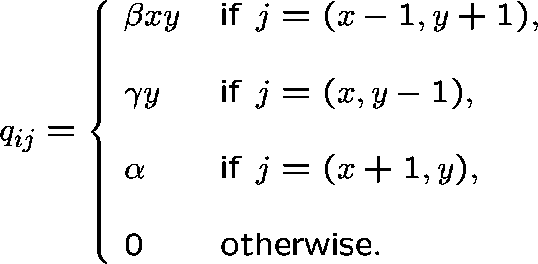
(Download the following image (as postscript)):
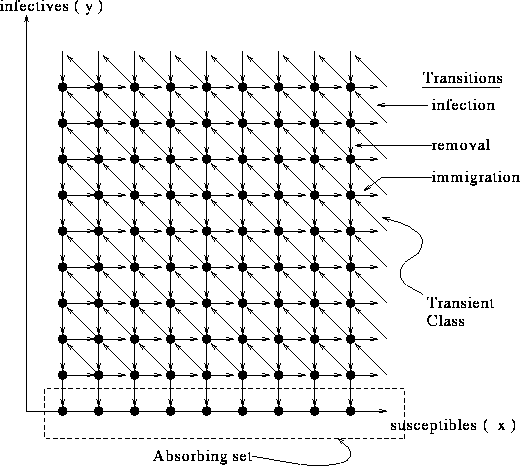
Figure 3. State transition diagram for
Ridler-Rowe epidemic model.
Clearly,
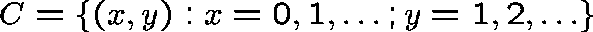
is an irreducible transient class.
Ridler-Rowe (1967): Q is regular (nonexplosive) and absorption occurs with probability 1.
(Download the following image (as postscript)):
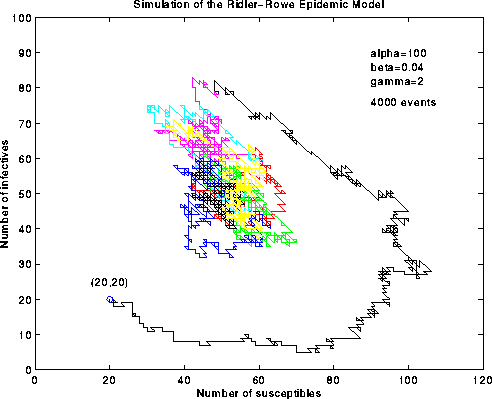
Figure 4. Simulation of the Ridler-Rowe epidemic model
[Simulation |
java code]
(Download the following image (as postscript)):

Figure 5. Simple contour plot of the usual diffusion
approximation for the Ridler-Rowe epidemic model
(to be imagined as superimposed on Figure 4)
(Download the following image (as postscript)):
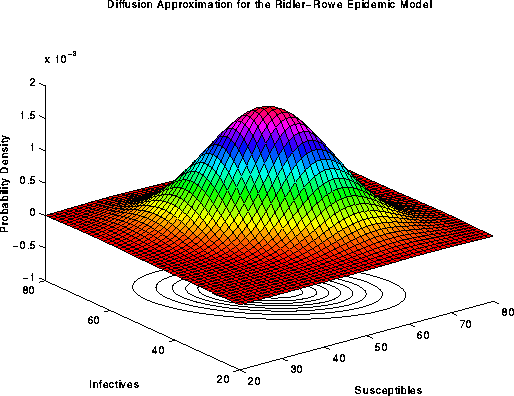
Figure 6. Surface plot of the usual diffusion
approximation for the Ridler-Rowe epidemic model
QUASISTATIONARY DISTRIBUTIONS
Notation. Let 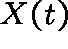 be the state of the system at time t and
suppose that
be the state of the system at time t and
suppose that 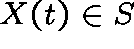 , where S, the state space, is a discrete
set. Let
, where S, the state space, is a discrete
set. Let 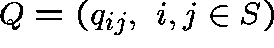 be the matrix of transition rates
(q-matrix), so that
be the matrix of transition rates
(q-matrix), so that 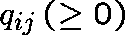 , for
, for 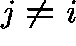 , represents
the transition rate from state i to state j and
, represents
the transition rate from state i to state j and 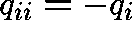 ,
where
,
where 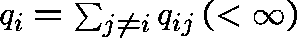 represents the transition
rate out of state i.
represents the transition
rate out of state i.
Assumptions. Take 0 to be the sole absorbing state, that is,
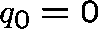 , and suppose that
, and suppose that 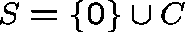 , where
, where 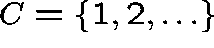 is an irreducible class. In order that there be a positive probability
of ever reaching 0, given that the process starts in C, suppose that
is an irreducible class. In order that there be a positive probability
of ever reaching 0, given that the process starts in C, suppose that
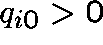 for at least one
for at least one 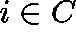 .
.
Let 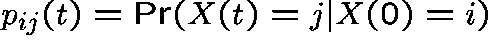 ,
, 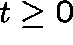 .
.
Definition.
Let 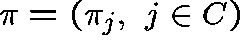 be a probability distribution over C and let
be a probability distribution over C and let
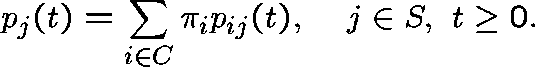
Then, 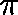 is a quasistationary distribution
if
is a quasistationary distribution
if
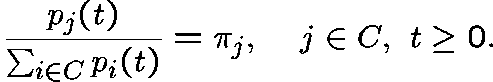
That is, if the process has 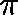 as its initial distribution, then
as its initial distribution, then  is a
quasistationary distribution
if the state probabilities at time t, conditional on the process
being in C at t, are the same for all t.
is a
quasistationary distribution
if the state probabilities at time t, conditional on the process
being in C at t, are the same for all t.
If  is a quasistationary distribution
then, under certain conditions,
is a quasistationary distribution
then, under certain conditions,
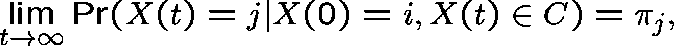
no matter what the value of 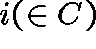 .
.
A CHARACTERIZATION
If 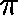 is a quasistationary distribution,
then clearly
is a quasistationary distribution,
then clearly
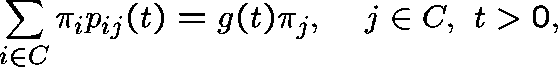
where 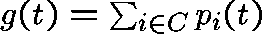 .
It is easy to show that g satisfies:
.
It is easy to show that g satisfies:
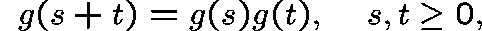
and 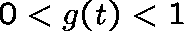 .
Thus,
.
Thus, 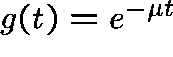 , for some
, for some  .
Since the converse is also true,
we have the following result:
.
Since the converse is also true,
we have the following result:
Proposition.
A probability distribution, 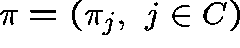 , over C
is a quasistationary distribution
if and only if, for some
, over C
is a quasistationary distribution
if and only if, for some  ,
, 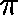 is a
is a 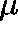 -invariant
measure, that is
-invariant
measure, that is
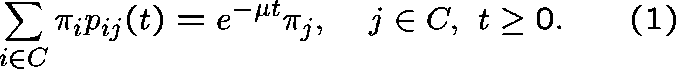
HOW DO WE DETERMINE 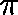 from Q?
from Q?
Rewrite (1) as
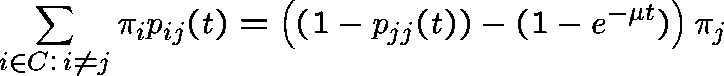
and remember that
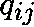 is the right-hand derivative of
is the right-hand derivative of 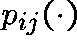 near 0.
So, on dividing by t and letting
near 0.
So, on dividing by t and letting 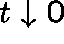 , we get (formally)
, we get (formally)
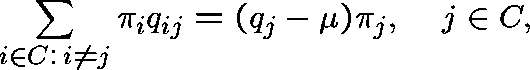
or, equivalently,
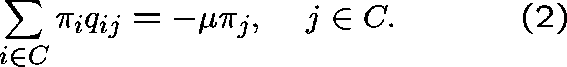
Accordingly, we shall say that 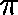 is a
is a 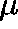 -invariant measure for
Q whenever (2) holds.
-invariant measure for
Q whenever (2) holds.
Proposition.
If 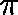 is a quasistationary distribution
then, for some
is a quasistationary distribution
then, for some  ,
, 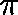 is a
is a 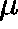 -invariant
measure for Q.
-invariant
measure for Q.
IS THE CONVERSE TRUE?
Suppose that, for some  ,
, 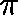 is a
is a 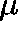 -invariant measure for
Q, that is
-invariant measure for
Q, that is
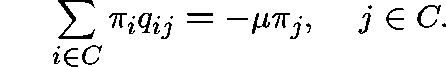
Is 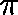 a quasistationary distribution?
a quasistationary distribution?
Sum this equation over 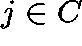 :
we get (formally)
:
we get (formally)
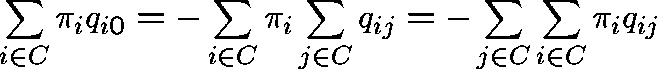
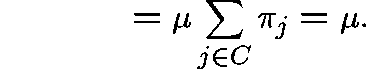
Theorem.
Let 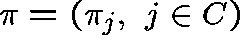 be a probability distribution
over C
and suppose that
be a probability distribution
over C
and suppose that 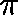 is a
is a 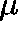 -invariant measure
for Q. Then,
-invariant measure
for Q. Then,
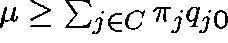 with equality if and only if
with equality if and only if 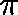 is a quasistationary distribution.
is a quasistationary distribution.
AN EXAMPLE
The birth-death-catastrophe process.
Let 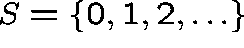 and suppose that
and suppose that
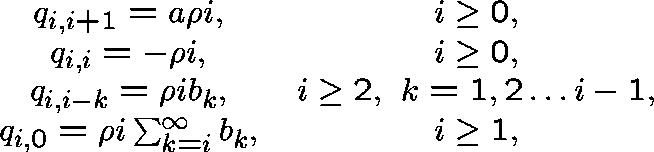
where  , a>0,
, a>0,
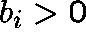 for at least one value of
for at least one value of 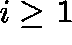 and
and
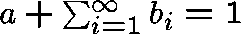 .
Thus, jumps occur at a constant ``per capita'' rate
.
Thus, jumps occur at a constant ``per capita'' rate 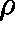 and,
at a jump time, a birth occurs with probability a, or
otherwise a catastrophe occurs, the size of which is determined by
the probabilities
and,
at a jump time, a birth occurs with probability a, or
otherwise a catastrophe occurs, the size of which is determined by
the probabilities 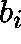 ,
, 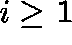 .
.
Clearly, 0 is an absorbing state and
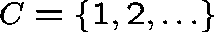 is an irreducible class.
is an irreducible class.
So, does the process admit a quasistationary distribution?
Substitute the transition rates in (2):
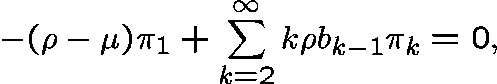
and, for 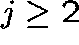 ,
,
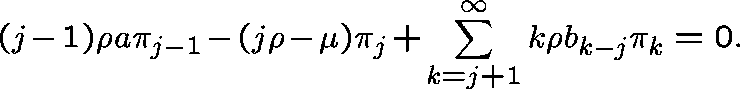
If we try a solution of the form 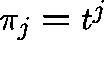 , the first equation tells us
that
, the first equation tells us
that 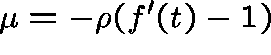 , where
, where
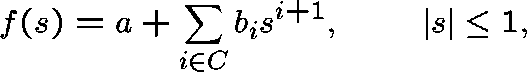
and, on substituting both of
these quantities in the second equation, we find that 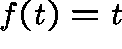 .
This latter equation has a unique solution,
.
This latter equation has a unique solution, 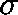 , on
, on 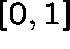 .
Thus, by setting
.
Thus, by setting 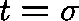 we can obtain a positive solution,
we can obtain a positive solution,
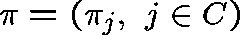 , to (2), such that
, to (2), such that 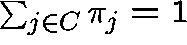 whenever
whenever 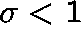 . Further, it is easy to
show that
. Further, it is easy to
show that 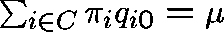 .
.
The condition 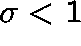 is satisfied only in the subcritical case,
that is, when the drift, D, given by
is satisfied only in the subcritical case,
that is, when the drift, D, given by
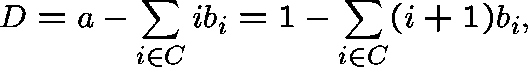
is strictly negative; incidentally, this also guarantees that absorption occurs with probability 1.
Proposition.
The subcritical birth-death-catastrophe process has a
geometric quasistationary distribution
, 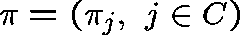 , given by
, given by
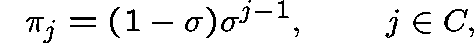
where 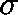 is the unique solution to
is the unique solution to 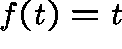 on the
interval
on the
interval 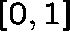 .
.
COMPUTATIONAL METHODS
Finite S : Mandl (1960) showed that the restriction of Q to
C has eigenvalues with negative real parts and the one with maximal
real part (called 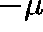 above) is real and has multiplicity 1, and,
the corresponding left eigenvector,
above) is real and has multiplicity 1, and,
the corresponding left eigenvector, 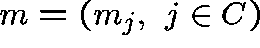 , has positive
entries; this is, of course, a
, has positive
entries; this is, of course, a 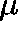 -invariant measure for Q (unique
up to constant multiples). Since S is finite, the quasistationary distribution,
-invariant measure for Q (unique
up to constant multiples). Since S is finite, the quasistationary distribution,
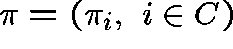 , exists and is given by
, exists and is given by
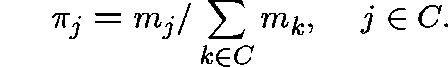
Infinite S : Truncate the restriction of Q to an  matrix,
matrix, 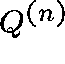 , and construct a sequence,
, and construct a sequence, 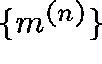 , of
eigenvectors and hope that this converges to a
, of
eigenvectors and hope that this converges to a 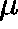 -invariant measure, m,
for Q, et cetera.
-invariant measure, m,
for Q, et cetera.
HOW SHOULD WE EVALUATE m?
Consider the Ridler-Rowe epidemic model.
First truncate C to
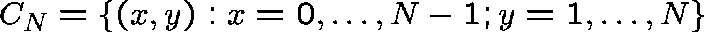
and restrict Q to 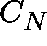 .
Use the transformation
.
Use the transformation
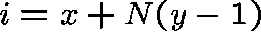 to convert the restricted q-matrix into an
to convert the restricted q-matrix into an  matrix,
matrix, 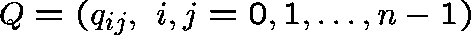 , where
, where 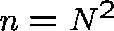 .
.
Evaluation of the eigenvectors of Q is not completely
trivial. For example, if (as well shall assume) N=100,
that is 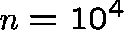 , Q needs 400 Mbytes of storage.
, Q needs 400 Mbytes of storage.
However, for N large, this matrix is large and sparse. Does this help?
THE ARNOLDI METHOD
We need to solve 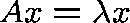 , where
, where 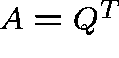 .
.
Using an initial estimate of x, the basic Arnoldi method produces an
 (upper-Hessenberg) matrix
(upper-Hessenberg) matrix 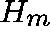 and an
and an
 matrix
matrix 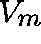 with
with
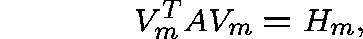
and such that if 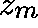 is an eigenvector of
is an eigenvector of
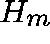 , then, for m large,
, then, for m large, 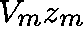 is close
to an eigenvector of A.
is close
to an eigenvector of A.
Solve for 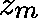 using standard (dense-matrix) methods.
using standard (dense-matrix) methods.
AN ITERATIVE ARNOLDI METHOD
Take m small (we found that m=20 worked best).
Then,
using an initial estimate, 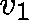 , of the eigenvector x,
apply the basic Arnoldi method (to obtain
, of the eigenvector x,
apply the basic Arnoldi method (to obtain 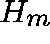 and
and 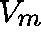 ) and
set
) and
set 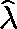 to be the dominant eigenvalue of
to be the dominant eigenvalue of 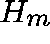 if this is real, or set
if this is real, or set 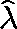 equal to zero otherwise.
equal to zero otherwise.
Now solve
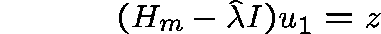
with z chosen at random and repeat the procedure with a new initial estimate, given by
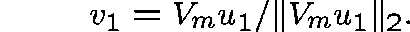
Continue until the residual, 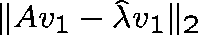 , is
sufficiently small.
, is
sufficiently small.
(Download the following image (as postscript)):
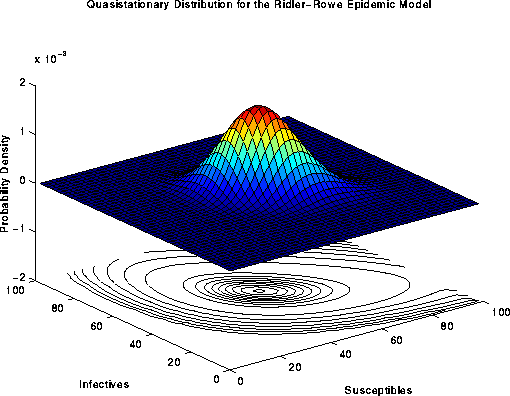
Figure 7. Surface plot of the quasistationary distribution
for the Ridler-Rowe epidemic model
(Download the following image (as postscript)):
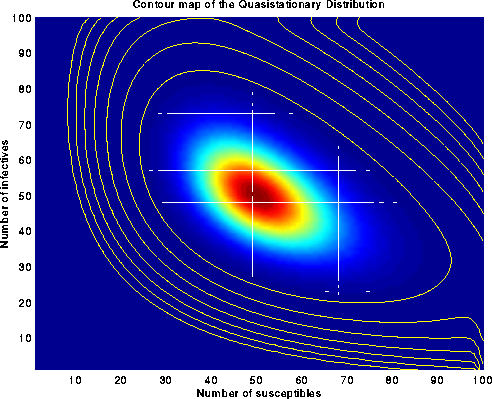
Figure 8. Contour plot of the quasistationary distribution
for the Ridler-Rowe epidemic model
(Download the following image (as postscript)):
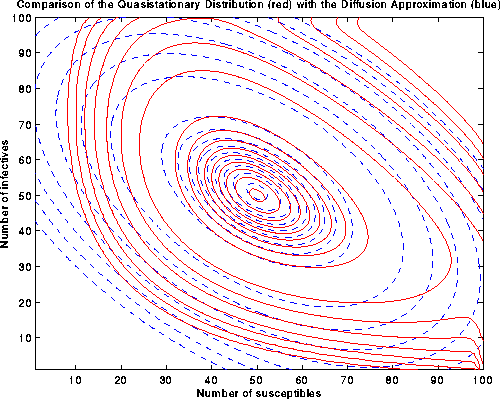
Figure 8. Comparison between the quasistationary distribution
and the diffusion approximation (contour plot) for the
Ridler-Rowe epidemic model
(Download the following image (as postscript)):
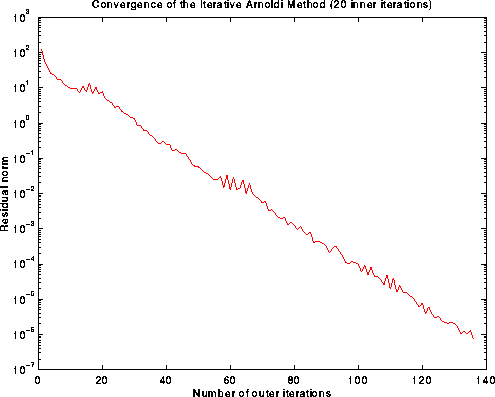
Figure 10. Graph of the residual norm versus the
number of outer iterations for the
Iterative Arnoldi Method
(Download the following image (as postscript)):
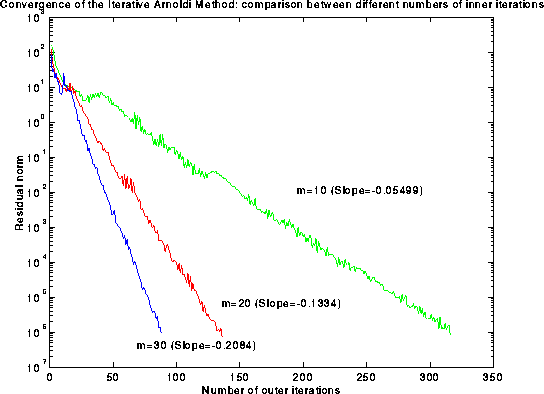
Figure 11. Graph of the residual norm versus the
number of outer iterations for various
values of m, the number of inner iterations