is a continuous time
Markov chain with a discrete state space
,
where 0 is the state corresponding to extinction
and 
comprises the remaining states.
LIMITING CONDITIONAL DISTRIBUTIONS FOR STOCHASTIC METAPOPULATION MODELS
by
Phil Pollett
Department of Mathematics
The University of Queensland
CONDITIONAL STATE DISTRIBUTION
X(t) - state of the population at time t
We suppose that
- state probabilities
We observe the population at an arbitrary time u and extinction has not yet occurred. How can we incorporate this information?
The conditional state distribution
Evaluate the state probabilities at time u conditioned on non-extinction:
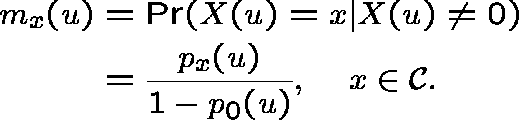
A STOCHASTIC MODEL FOR METAPOPULATIONS
There are n geographical regions (patches):
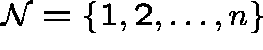Let 
,
where 
is 1 or 0 according as patch i is
occupied or not at time t ( 
).
Note that the state space is 
.
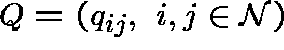- Interaction matrix:
, for
, is the probability that patch j will not be colonized by migration from patch i, and
is the probability that (in the absence of immigration) patch i will become extinct.
Assume (Gyllenberg and Silvestrov) that
where 
is the distance between patches i
and j ( 
and 
),
is the area of patch i
and a( 
) measures how badly individuals are at migrating.
THE TRANSITION PROBABILITIES
Assume that the various colonization processes and local extinction
processes are independent. Define 
, where
, by
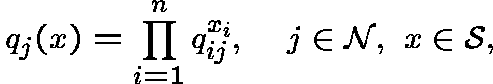
to be the probability that patch j will become extinct at the next epoch given a present configuration x.
The transition matrix 
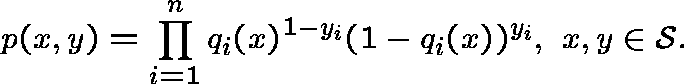
Note that, since 
, 
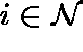, state 
(corresponding to the extinction of all patches) is an absorbing state
for the chain:
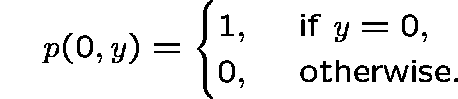
A 5-PATCH METAPOPULATION
Patches 2, 3, 4 & 5 are equally
spaced (a distance 0.1 apart), while Patch 1 is 10 times that distance away
from the others ( 
).
All patches have the same area.
PERSISTENCE OF METAPOPULATIONS: QUASI-STATIONARITY
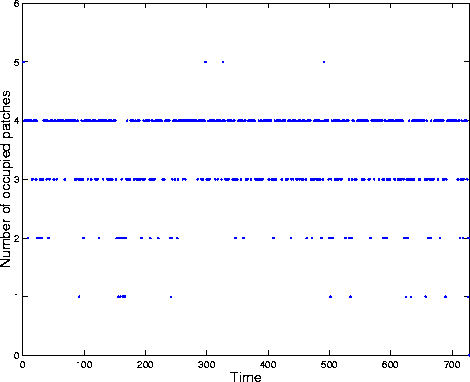
Simulation of the 5-patch model with a=7. The number of occupied patches is plotted against time (up to extinction at t=728).
Do the conditional state probabilities account for the observed behaviour?
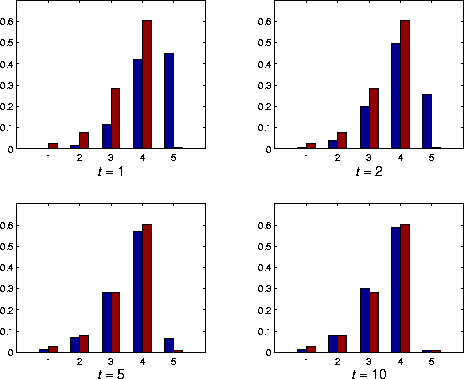
Comparison of the observed frequencies with the conditional state
distribution 
at t=1,2,5,10.
The brown
bar is the proportion of time for which i patches were occupied
( 
) during the period of the simulation.
The blue bar is the distribution
of the number of occupied patches evaluated using .
LIMITING CONDITIONAL DISTRIBUTIONS
The observed trend has a simple theoretical
explanation. Since is a finite set, the limit
exists and defines a proper distribution 
, called a
limiting conditional distribution, and m is the left
eigenvector of 
(P restricted to ) corresponding to the
eigenvalue, 
, with maximal modulus
(Darroch and Seneta (1965)).
Note that the expected time till absorption, 
, is approximately
.
We can be precise about the rate of
convergence by examining the eigenvalue, 
, of
with second-largest modulus. It might not
be real, and it has multiplicity 
(for simplicity, suppose 
). It can be
shown that
where 
.
THE CONVERGENCE OF TO 
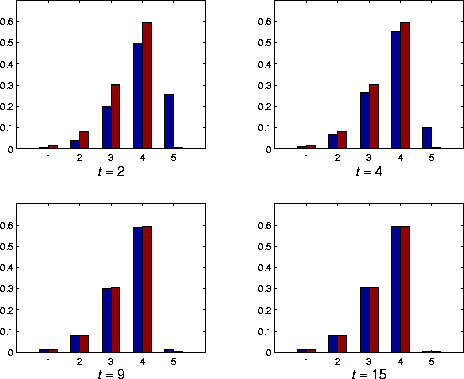
Comparison between the conditional state distribution (blue) and the limiting conditional distribution (brown) of the number of occupied patches for the 5-patch metapopulation model with a=7.
For the 5-patch metapopulation model with a=7, we
find that 
, 
(real with
multiplicity 1), 
and 
.
PSEUDO-STATIONARY DISTRIBUTIONS
(The method of Gyllenberg and Silvestrov)
Rationale: If we had assumed that Patch 1 (say) had
a zero local extinction probability ( 
), that patch would
behave as a mainland. State 0 would no
longer be accessible from all states: would decompose
into two classes, 
and 
, consisting of those
states in which have 
and 
respectively; either the
process would start in (mainland inhabited) and remain
there, or, start in (mainland uninhabited) and eventually
enter either or the absorbing state.
We identify a ``quasi-mainland'', namely a single patch i
with small (say Patch 1), and consider a sequence of
processes indexed by 
, treating 
as a
perturbation.
PERTURBATION THEORY
Let 
(now arbitrary) and suppose that our interaction
matrix depends on in the following way:
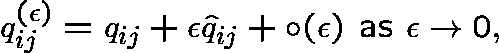
where
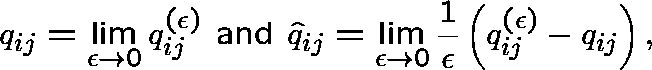
the latter assumed to be non-negative and finite, and, that 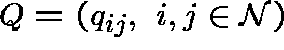satisfies .
Then, in an obvious notation,
where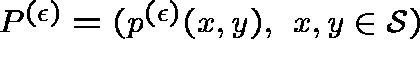 
is the
transition matrix corresponding to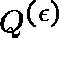 
and is the transition matrix corresponding to Q.
THE G&S LIMITING REGIME
Let 
and 
in such a way that
, where 
.
Since the expected lifetime of the
quasi-mainland is of order 
, one is able to study the
process on different time scales
(s=0, 
, and 
).
G&S showed that the limit
exists and is given by a mixture of the limiting probabilities
for the (ergodic) chain generated by Q and the degenerate
distribution 
which assigns all its mass to state 0, the
mixing probability being 
, where 
is a positive
constant which is specified in terms of 
.
A COMPARISON USING THE 5-PATCH MODEL
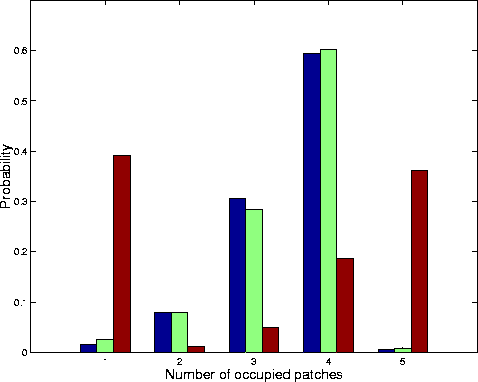
Comparison between the limiting conditional distribution (blue), the simulated proportions (green) and the pseudo-stationary distribution (brown).
The disparity is marked: for this example, the two ways of analysing the model lead to quite different predictions.
THE EFFECT OF VARYING s
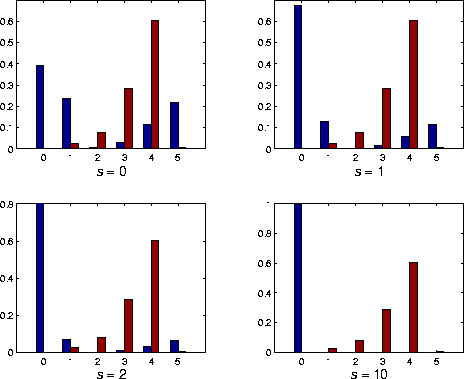
The effect of varying s on the pseudo-stationary distribution (blue). The brown bar represents the simulated proportions of occupied patches.
Observe that the disparity becomes worse as the time-scale parameter s increases.
RECONCILIATION
Denote the state probabilities corresponding to 
by
,
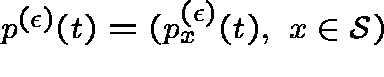and denote the corresponding conditonal probabilities by
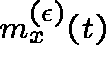. Gosselin (1997) proved that
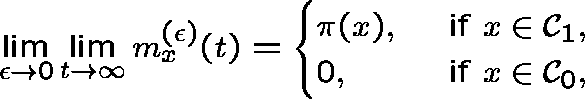
which he compared with Theorem 6.2 of G&S:
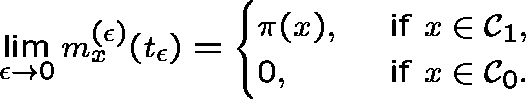
Thus, in the important case
s=0, the limiting conditonal distribution and the pseudo-stationary
agree when is small.
The problem with the 5-patch model is that 
- not sufficiently small.
REMARKS
Quasi-stationarity is a property of the model
and not the means of analysing it. The 5-patch model exhibits
quasi-stationarity, demonstrated emphatically using simulation, yet
is not small. The pseudo-stationary distribution does not
capture this behaviour. On the other hand, the conditional state
distribution m(t) does: afterall, it is the most information our
model can provide at any time t given that we know extinction has
not occured by time t. In cases when the convergence of m(t) to the
limiting conditional distribution m is rapid, this
distribution can be used instead.