TRAFFIC PROCESSES
Traffic process  :
:  is the (cumulative)
number of arrivals in
is the (cumulative)
number of arrivals in  . Assume that
. Assume that  and that no two
calls can arrive at exactly the same time.
and that no two
calls can arrive at exactly the same time.
If N were a Poisson process
(with rate  ), then
), then
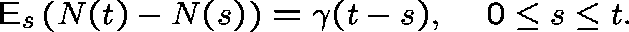
or, more generally,

Here  represents expectation conditional on the
past at time s
(formally,
represents expectation conditional on the
past at time s
(formally,  , where
, where  is an
increasing, right-continuous family of
is an
increasing, right-continuous family of  -algebras, with
-algebras, with  being
being
 measurable and
measurable and  being complete).
being complete).
We say that N has a deterministic past-conditional arrival rate.
WATANABE'S THEOREM
Now let N be an arbitrary traffic process.
Theorem If N has a deterministic past-conditional arrival rate, then N is a Poisson process.
Outline Proof For simplicity, suppose that
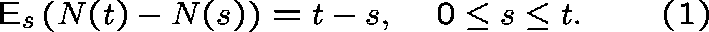
Now extend (1) to stopping times  and
and  with
with
 as follows:
as follows:
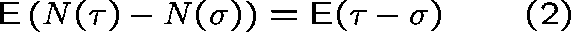
(recall that  is a stopping time if
is a stopping time if
 ). Let
). Let  be
the sequence of arrival times, and, for fixed i, define
be
the sequence of arrival times, and, for fixed i, define
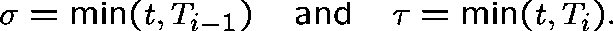
Consider the three possible cases
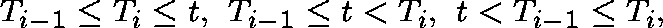
and observe that
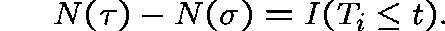
Thus,
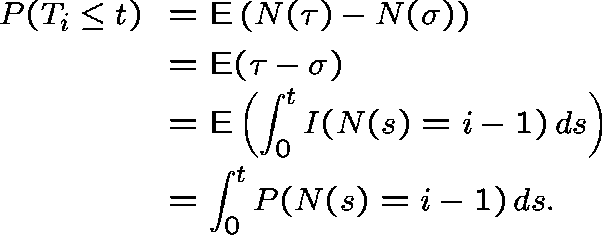
Setting  we find that
we find that
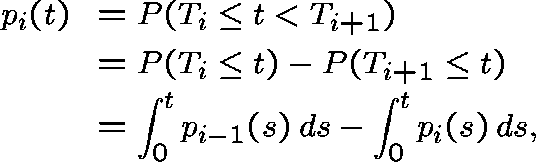
and hence that  .
.
For i=0 we get
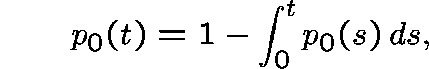
which gives  . Since
. Since  we deduce that
we deduce that  has a Poisson distribution with parameter t.
has a Poisson distribution with parameter t.
We also require  to be independent of the
past at s. Fix s and
to be independent of the
past at s. Fix s and  , and let
, and let  . Then,
(2) gives
. Then,
(2) gives
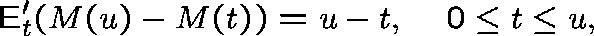
where  refers to expectation conditional on the past at time t,
including the fixed event A. But the previous analysis then
gives a Poisson
refers to expectation conditional on the past at time t,
including the fixed event A. But the previous analysis then
gives a Poisson distribution for
distribution for  , that is, a Poisson
distribution with parameter t for
, that is, a Poisson
distribution with parameter t for  , conditional on A.
This establishes the required independence.
, conditional on A.
This establishes the required independence.
CONDITIONAL INTENSITY
Let  be an arbitrary traffic process.
be an arbitrary traffic process.
Under mild regularity conditions, the limit
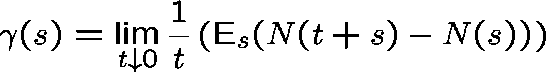
exists and defines the conditional intensity (process),
 , and, if we set
, and, if we set
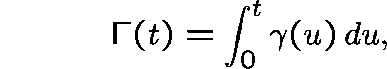
then, for all  ,
,
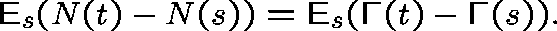
For stopping times  and
and  such that
such that  ,
,

where  means expectation conditional on the past at time
means expectation conditional on the past at time  :
formally, the
:
formally, the  -algebra of events, A,
such that
-algebra of events, A,
such that  for each t.
for each t.
POISSON APPROXIMATIONS
Let N be a traffic process with conditional intensity  . Fix
. Fix
 and let A be an event determined by N on
and let A be an event determined by N on  . It is
proposed to approximate
. It is
proposed to approximate  by
by  , where
, where  is the
probability that A would have if N were Poisson with given rate
is the
probability that A would have if N were Poisson with given rate  .
.
The idea is to construct a Poisson process M using N.
Define  , the (pseudo) inverse
of the increasing (random) function
, the (pseudo) inverse
of the increasing (random) function  . In general
. In general
 , but
, but  , with inequality
occurring at only those t for which
, with inequality
occurring at only those t for which  is constant around an interval
containing t. Certainly
is constant around an interval
containing t. Certainly  for
for  , and so we may apply
the above (stopping time) result, namely
, and so we may apply
the above (stopping time) result, namely
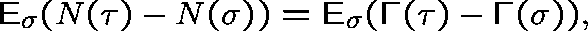
with  and
and  .
.
This gives

 .
.
Thus, by the previous argument,  is a unit-rate Poisson
process and so M, where
is a unit-rate Poisson
process and so M, where  , is a Poisson
process with rate
, is a Poisson
process with rate  .
A familiar coupling argument then leads to the following result:
.
A familiar coupling argument then leads to the following result:
Proposition For arbitrary A,
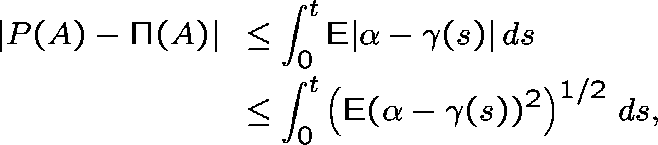
where  is the probability that A would have if the traffic
process were Poisson with parameter
is the probability that A would have if the traffic
process were Poisson with parameter  .
If the traffic process is stationary
with
.
If the traffic process is stationary
with  , then
, then
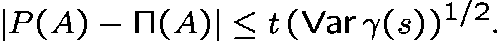
A STAR NETWORK
There are K outer nodes which communicate via a single central node.
Thus, there are K links (circuit groups),
and each route consists of a pair of links  .
.
Assume that
-
the links have C circuits,
-
calls arrive as independent Poisson processes,
-
these have the same rate,
 ,
,
-
call lengths are exponential with mean 1,
-
these are mutually independent.
Keep the total offered traffic,  , (to the network)
fixed and let the number of
switching nodes, K, become large; what happens?
, (to the network)
fixed and let the number of
switching nodes, K, become large; what happens?
A POISSON APPROXIMATION FOR THE
STAR NETWORK
Let  be the number of calls offered to link k in the
time-interval
be the number of calls offered to link k in the
time-interval  and let
and let  be the number of circuits in use on link j at time s.
Clearly
be the number of circuits in use on link j at time s.
Clearly  , the conditional intensity of
, the conditional intensity of  , is given by
, is given by
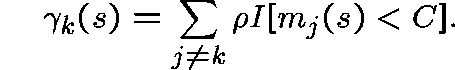
Thus  and
and



Recall that if A is any event determined by  on
on  , then
, then
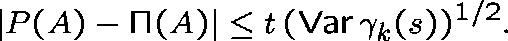
ASYMPTOTICALLY INDEPENDENT BLOCKING
Proposition (Ziedins and Kelly (1989)):
By keeping the total offered traffic,  , fixed and letting the
number of switching nodes, K, become large, the links are blocked
independently.
Specifically, as
, fixed and letting the
number of switching nodes, K, become large, the links are blocked
independently.
Specifically, as  ,
,

We deduce that the traffic offered to any given link is approximately Poisson, since



 .
.
A MARKOVIAN QUEUEING NETWORK
Label the links  and
make the usual simplifying assumptions:
and
make the usual simplifying assumptions:
-
the links are perfectly reliable and are not subject to noise, so that
message transmission times are determined by their length.
-
the time taken by the nodes to switch, and, if necessary, buffer,
reassemble and acknowledge
messages, is negligible in comparison with their transmission times.
- traffic entering the network from external sources is Poisson and message lengths are mutually independent and exponentially distributed with mean 1.
A total effort (or capacity) of  is provided by link j when there
are n messages whose transmission is incomplete.
is provided by link j when there
are n messages whose transmission is incomplete.
A POISSON APPROXIMATION
Let  be the net traffic offered to a given link,
k, on the interval
be the net traffic offered to a given link,
k, on the interval  .
Since all messages have unit mean length, the rate at which messages are
transmitted by link j is
.
Since all messages have unit mean length, the rate at which messages are
transmitted by link j is  when there are n messages present.
Thus, if
when there are n messages present.
Thus, if  is the number of messages present at link j at time s,
then
is the number of messages present at link j at time s,
then  , the conditional intensity of
, the conditional intensity of  , is given by
, is given by

where  is the rate of externally offered traffic
and
is the rate of externally offered traffic
and  is the proportion of messages emanating from
link j which next use link k.
is the proportion of messages emanating from
link j which next use link k.
Let  . Then (in equilibrium)
. Then (in equilibrium)
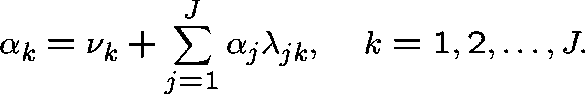
An equilibrium exists if and only if, for each j,

in which case, the states of the individual links are independent and the probability that there are n messages at link j is given by
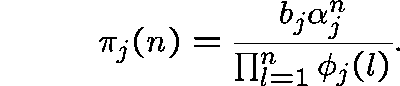
We can then show that

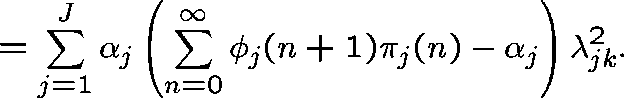
This leads to a bound on the degree of deviation of
 from a Poisson process with rate
from a Poisson process with rate  .
.
STATE-INDEPENDENT CAPACITY
Suppose

Then
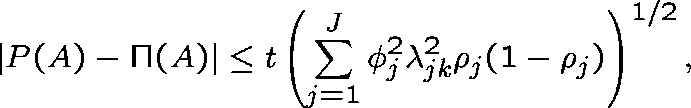
where  (we must have that
(we must have that  ).
Thus, if for each j,
).
Thus, if for each j,  is
is  and either
and either
- (1)
-
 is
is  ,
,
- (2)
-
 is
is  , or
, or
- (3)
-
 is
is  ,
,
then the Poisson approximation is sure to be good.
SIMULTANEOUS APPROXIMATIONS
BY INDEPENDENT POISSON PROCESSES
Let  be l traffic processes and let
be l traffic processes and let
 be their conditional intensities.
be their conditional intensities.
If A is an event which is determined by these processes on the interval
 and
and  is the probability that A would have if
these processes were independent
Poisson processes with
rates
is the probability that A would have if
these processes were independent
Poisson processes with
rates  , then
, then
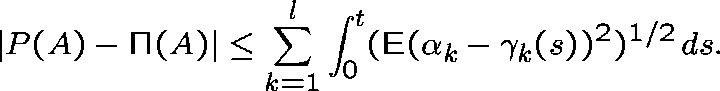
If the system is in equilibrium
and  are chosen such that
are chosen such that
 , then a simpler bound is given by
, then a simpler bound is given by
