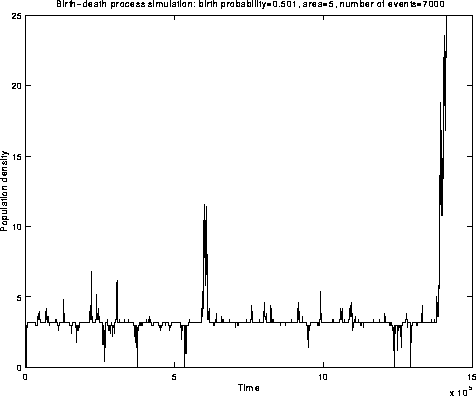
Quasistationarity in continuous-time Markov chains with positive drift
by
Pauline Coolen-Schrijner, The University of Durham
Andrew Hart, The University of Queensland
Phil Pollett, The University of Queensland

Fig.1: The behaviour we seek to describe
MARKOV CHAINS WITH POSITIVE DRIFT
Let ![]() be a continuous time Markov chain over a denumerable
state space S. For simplicity take
be a continuous time Markov chain over a denumerable
state space S. For simplicity take ![]() .
.
Let ![]() be the matrix of transition rates
(q-matrix), assumed to be stable and conservative,
so that
be the matrix of transition rates
(q-matrix), assumed to be stable and conservative,
so that ![]() , for
, for ![]() , represents the
transition rate from state i to state j and
, represents the
transition rate from state i to state j and ![]() , where
, where
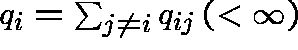 represents the transition rate
out of state i.
represents the transition rate
out of state i.
Let ![]() , where
, where
![]()
and suppose that 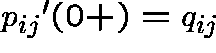 .
It will not be necessary to assume that the transition function P is
determined uniquely by Q.
.
It will not be necessary to assume that the transition function P is
determined uniquely by Q.
We assume only that P is irreducible, that is, ![]() for all
for all ![]() ,
and transient, that is,
,
and transient, that is,
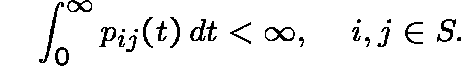
LIMITING CONDITIONAL DISTRIBUTIONS
We shall be concerned with the existence of a limiting conditional distribution (LCD) for the process:
![]()
The conditional probability can be evaluated as follows:
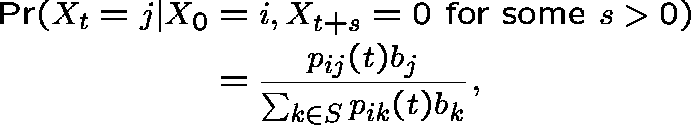
where
![]()
Note that ![]() and (by
irreducibility and transience)
and (by
irreducibility and transience) ![]() ,
, ![]() .
.
LCDs for ABSORBING CHAINS
Compare the above definition with the widely studied LCDs for absorbing chains:
Append to S an absorbing state (or, more generally, an absorbing
set) ![]() such that
such that ![]() for some (and then all)
for some (and then all)
![]() and t>0.
and t>0.
In this context we study the limit (as ![]() ) of
) of
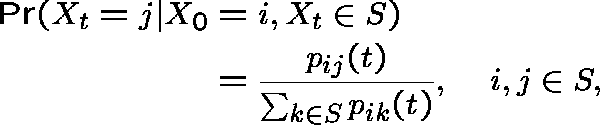
or, more generally (when ![]() , the probability of
absorption starting in j, is less than 1),
, the probability of
absorption starting in j, is less than 1),
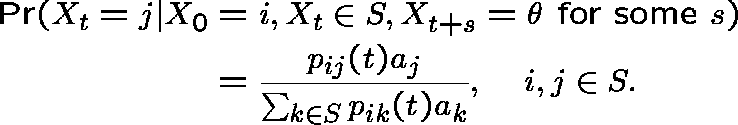
HITTING PROBABILITIES
Let ![]() , so
that
, so
that ![]() . This can be evaluated as
. This can be evaluated as
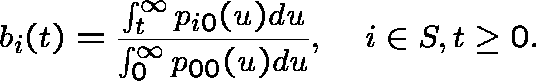
Claim.
![]() ,
, ![]() ,
, ![]() .
.
It follows that ![]() is a subinvariant vector for P;
in particular,
is a subinvariant vector for P;
in particular,
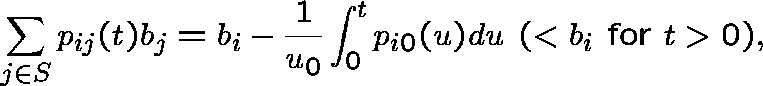
where 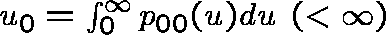 .
.
Claim. b is a subinvariant vector for Q; in fact, b is `almost invariant':
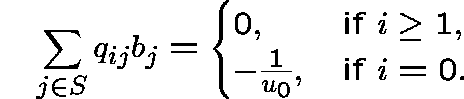
CONSTRUCTION OF THE DUAL
Define
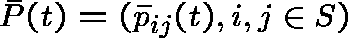 and
and
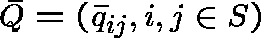 by
by
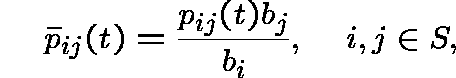
and
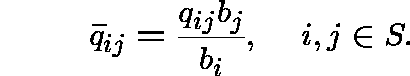
Clearly ![]() is a (standard) transition function
and
is a (standard) transition function
and ![]() is a q-matrix such that
is a q-matrix such that 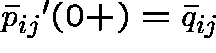 .
However, P is dishonest with
.
However, P is dishonest with
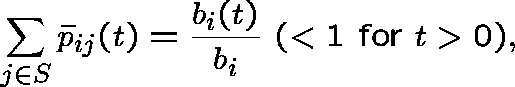
and ![]() is non-conservative with
is non-conservative with
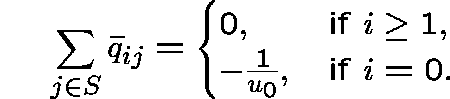
(Recall that ![]() .)
.)
CONSTRUCTION OF THE DUAL
Append to S an absorbing state
![]() and extend the definition
of
and extend the definition
of ![]() and
and ![]() to
to 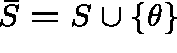 as follows:
as follows:
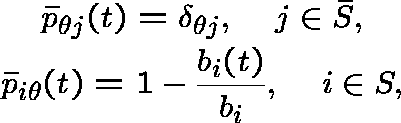
and
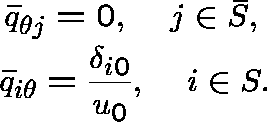
In this way ![]() will be conservative and
will be conservative and
![]() will be honest.
will be honest.
![]() is a
is a ![]() -transition function since, for
-transition function since, for ![]() ,
,
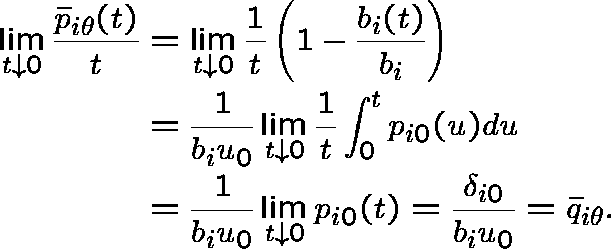
INTERPRETATION OF THE DUAL
Let L be the last exit time of state 0, that is,
![]()
and define 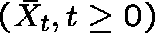 by
by
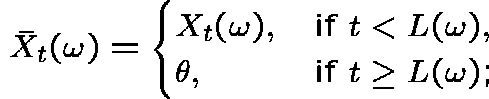
![]() is
is ![]() killed at time L.
Then
killed at time L.
Then![]() ,
since
,
since ![]() ,
,
![]() is Markovian with transition function
is Markovian with transition function ![]() , and,
if
, and,
if ![]() , its initial distribution is given by
, its initial distribution is given by
Notice that ![]() is absorbed with probability 1:
is absorbed with probability 1:
EXISTENCE OF LCDs
By the definition of ![]() , we see immediately that,
for every
, we see immediately that,
for every ![]() ,
,

Here is one such result for absorbing chains:
Theorem. Suppose S is ![]() -positive
recurrent and let
-positive
recurrent and let ![]() be the (essentially unique)
be the (essentially unique)
![]() -invariant measure for
-invariant measure for ![]() . Then, if
. Then, if
![]() ,
,
![]() -CLASSIFICATION
-CLASSIFICATION
![]() and P have the same
and P have the same
![]() -classification.
-classification.
The decay parameter:
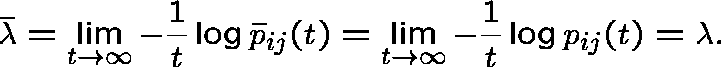
Note that ![]() (
( ![]() ) is the same for each
) is the same for each ![]() and
and
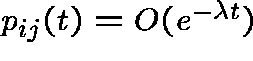 ,
, 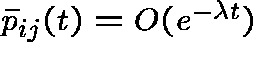 .
.
Geometric ergodicity:  .
.
![]() -transience/recurrence:
for
-transience/recurrence:
for ![]() ,
,

![]() -positive/null recurrence:
for
-positive/null recurrence:
for ![]() ,
,

![]() -INVARIANT MEASURES FOR P
-INVARIANT MEASURES FOR P
Definition. A collection of positive numbers
![]() is called a
is called a ![]() -subinvariant measure
for P if, for all
-subinvariant measure
for P if, for all ![]() ,
,
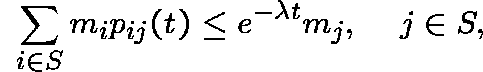
and ![]() -invariant if, for all
-invariant if, for all ![]() ,
,
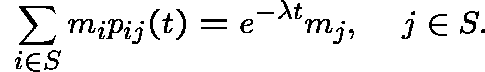
Now, for any given collection ![]() , define
, define ![]() by
by ![]() .
.
Claim. m is ![]() -(sub)invariant for P if and only if
-(sub)invariant for P if and only if
![]() is
is ![]() -(sub)invariant for
-(sub)invariant for ![]() .
.
Claim.
If m is a ![]() -subinvariant measure for P, then
-subinvariant measure for P, then
![]() if
if ![]() .
If m is
.
If m is ![]() -invariant for P, then
-invariant for P, then
![]() only if
only if ![]() .
.

![]() -INVARIANT MEASURES FOR Q
-INVARIANT MEASURES FOR Q
Definition. A collection of positive numbers
![]() is called a
is called a ![]() -invariant measure
for Q if, for all
-invariant measure
for Q if, for all ![]() ,
,
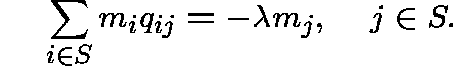
Again we have that m is ![]() -invariant for Q if and only if
-invariant for Q if and only if
![]() is
is ![]() -invariant for
-invariant for ![]() .
.
Now suppose that Q is regular, so that P, now being the unique Q-transition function, is honest.
We can then apply to ![]() the following result for absorbing chains
(with a transient class S and absorbing state
the following result for absorbing chains
(with a transient class S and absorbing state ![]() ):
):
Theorem.
If ![]() is a finite
is a finite ![]() -invariant
measure for
-invariant
measure for ![]() , then it is
, then it is ![]() -invariant for
-invariant for ![]() if and only if
if and only if
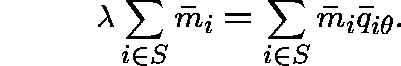
LCDs WHEN Q IS REGULAR
Theorem.
Let ![]() and suppose that
and suppose that ![]() is
a
is
a ![]() -invariant measure for Q. Then,
-invariant measure for Q. Then,
![]() , and
m is
, and
m is ![]() -invariant for P if (and only if)
-invariant for P if (and only if)
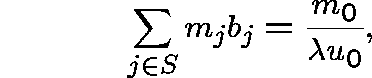
whence if S is ![]() -positive the LCD exists:
-positive the LCD exists:
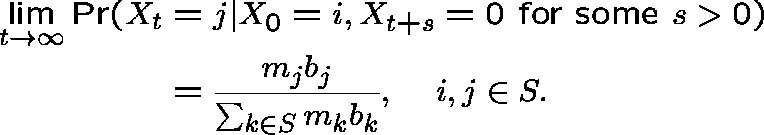
Other examples:
BIRTH-DEATH PROCESSES
Consider an irreducible
birth-death process on ![]() . Its q-matrix is given by
. Its q-matrix is given by
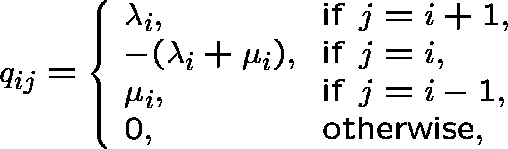
where ![]() (
( ![]() ),
),
![]() (
( ![]() ) and
) and ![]() .
.
Define series A and C by
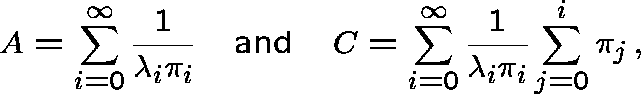
where ![]() and, for
and, for ![]() ,
,
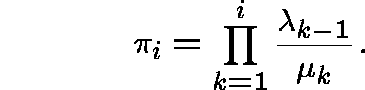
Assume that ![]() (Q regular) and
that
(Q regular) and
that ![]() (S transient). Then, the hitting probabilities
are given by
(S transient). Then, the hitting probabilities
are given by
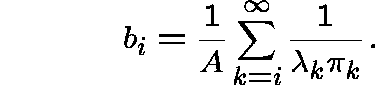
Define polynomials ![]() , where
, where ![]() ,
by
,
by ![]() ,
, ![]() and, for
and, for
![]() ,
,
![]() ,
and let
,
and let ![]() ,
, ![]() , where
, where ![]() is the
decay parameter of S. Then, m is the essentially unique
is the
decay parameter of S. Then, m is the essentially unique
![]() -invariant measure.
-invariant measure.
The dual is an absorbing birth-death process; we get (in an obvious notation):
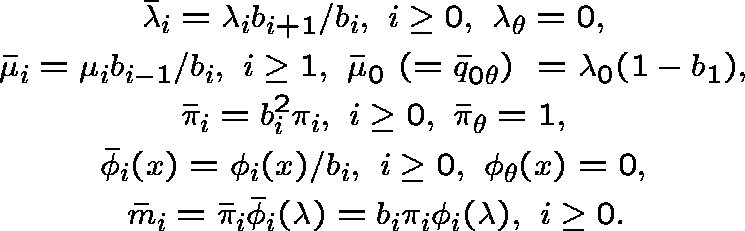
A direct application of van Doorn's![]() result for absorbing birth-death processes shows that
the LCD exists if and only if
result for absorbing birth-death processes shows that
the LCD exists if and only if ![]() :
:
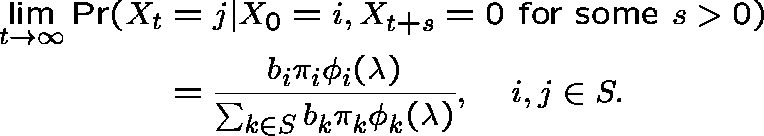
AN EXAMPLE
Let ![]() ,
V>0 and
,
V>0 and ![]() , and define
, and define ![]() ,
,
![]()
where ![]() .
.
This defines a density-dependent birth-death process
with constant jump probabilities: think of V as
``area'' and n/V as ``population density''.
The idea is that, as V gets large, the density process
![]() becomes ``more deterministic'':
becomes ``more deterministic'':
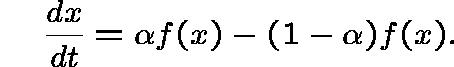
Clearly the process is irreducible if f(n)>0 for
all ![]() , and then transient if
(and only if)
, and then transient if
(and only if) ![]() , in which case
, in which case
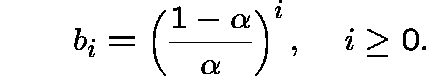
Two choices for f:
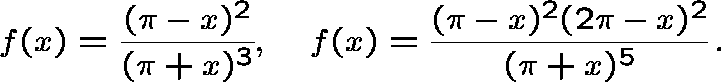
Each has ![]() and
and ![]() .
.

Fig.1: Simulation
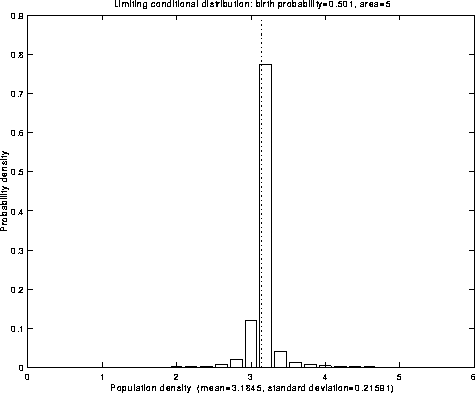
Fig.2: Limiting conditional distribution
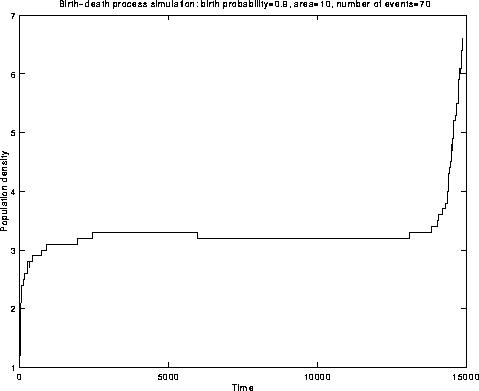
Fig.3: Simulation
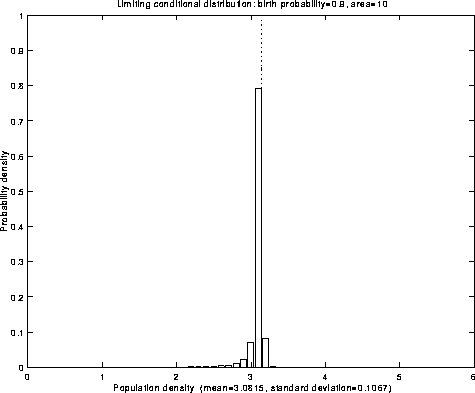
Fig.4: Limiting conditional distribution
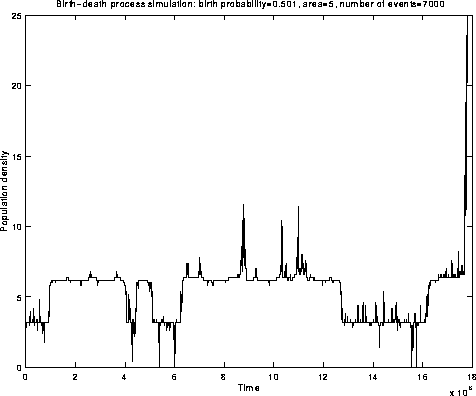
Fig.5: Simulation
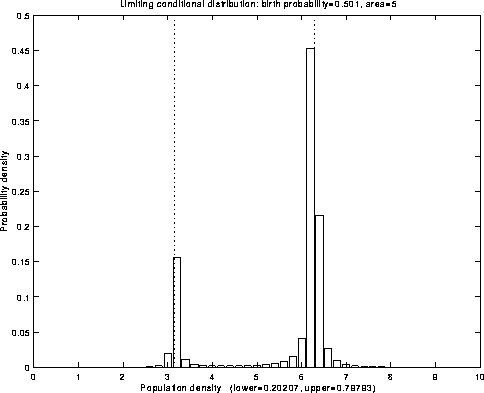
Fig.6: Limiting conditional distribution
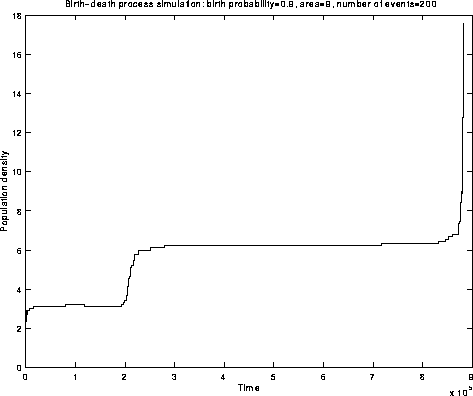
Fig.7: Simulation
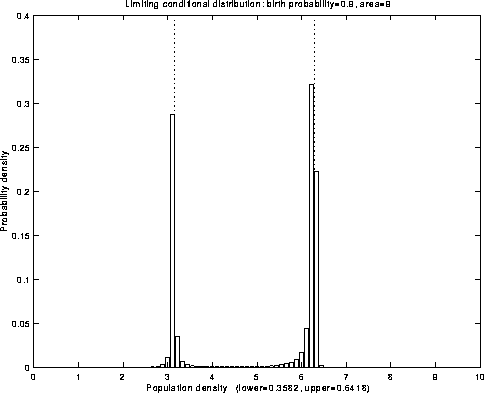
Fig.8: Limiting conditional distribution