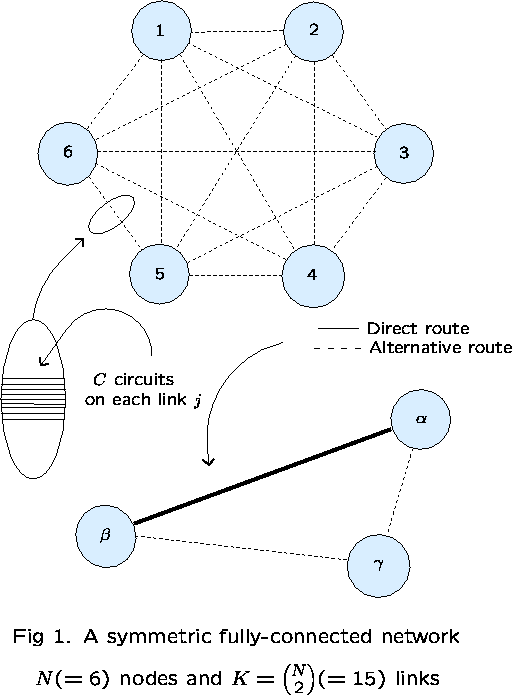
N - nodes
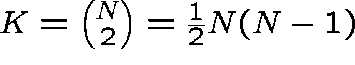 - links
- links
C - circuits on each link
Poisson traffic offered at rate ![]()
Exponentially distributed holding times
(mean 1)
r retries (initially take r=1)
MODELLING RANDOM FLUCTUATIONS
IN A BISTABLE TELECOMMUNICATIONS NETWORK
by
Phil Pollett
Department of Mathematics
The University of Queensland
1. Pollett, P.K., ``Modelling random fluctuations in a bistable telecommunications network'', Ed. W. Henderson, Proc. 7th Austral. Teletraffic Res. Seminar, (1992), 335-345.
2. Pollett, P.K., ``Diffusion approximations for a circuit switching network with random alternative routing'', Austral. Telecomm. Res. 25, (1992), 45-52.
3. Pollett, P.K., ``On a model for interference between searching insect parasites'' J. Austral. Math. Soc., Ser. B 31, (1990), 133-150.
4. Pollett, P.K. and Vassallo, A., ``Diffusion approximations for some simple chemical reaction schemes Adv. Appl. Probab. 24, (1992), 875-893.
N - nodes
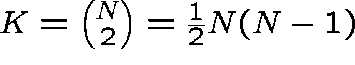 - links
- links
C - circuits on each link
Poisson traffic offered at rate ![]()
Exponentially distributed holding times
(mean 1)
r retries (initially take r=1)
Let 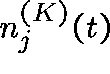 be the number of links with j circuits in
use at time t (for a network with K links).
be the number of links with j circuits in
use at time t (for a network with K links).
Let 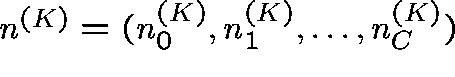 .
Then,
.
Then, 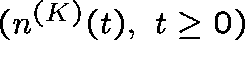 is a continuous-time
Markov chain which takes values in
is a continuous-time
Markov chain which takes values in
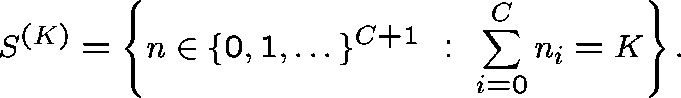
The transition rates, 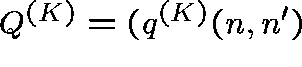 ,
, 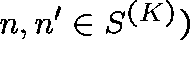 ,
of the process are given by
,
of the process are given by
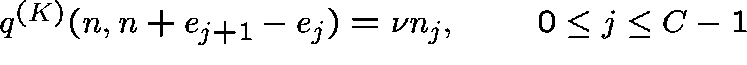 ,
,
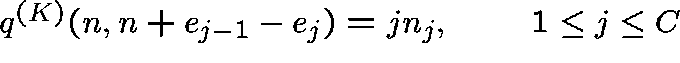 ,
,
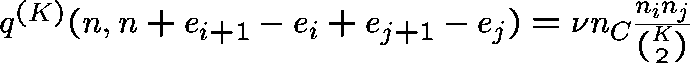 ,
,
![]() ,
,
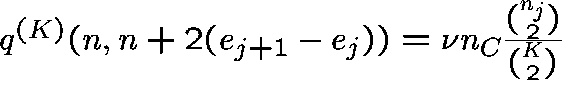 ,
,
![]() ,
,
where ![]() is the unit vector with 1 as its
is the unit vector with 1 as its ![]() entry.
entry.
Let 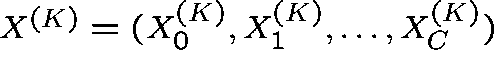 ,
where
,
where 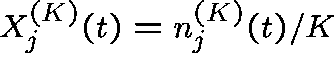 is the proportion of links with j circuits in use at time t.
The process
is the proportion of links with j circuits in use at time t.
The process 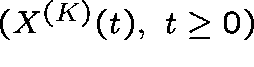 is itself a Markov chain, but one which
takes values in a lattice contained in the simplex
is itself a Markov chain, but one which
takes values in a lattice contained in the simplex
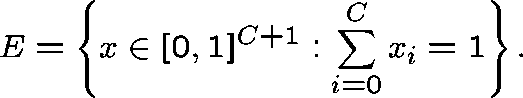
2-D ``SUMMARY'': 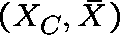
![]() is proportion of links full;
this estimates link blocking probability.
is proportion of links full;
this estimates link blocking probability.
And, 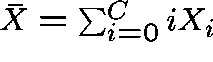 ;
this estimates the mean number of circuits in use
on any given link.
;
this estimates the mean number of circuits in use
on any given link.
If, as ![]() ,
,
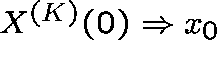 , then
, then
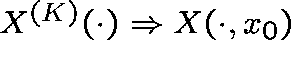 ,
where
,
where ![]() is a deterministic process with initial point
is a deterministic process with initial point ![]() and which satisfies
and which satisfies
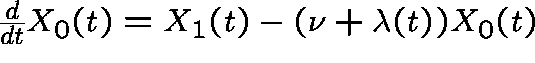 ,
,
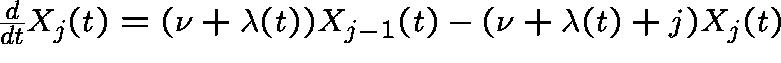
![]() ,
,
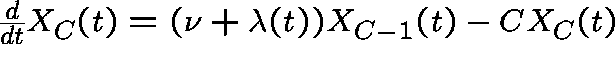 ,
,
where 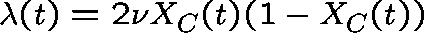 .
.
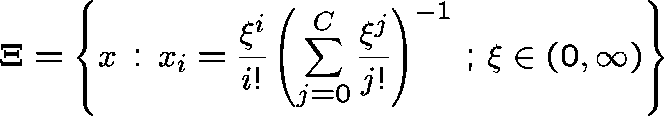
Theorem.
If, as ![]() ,
,
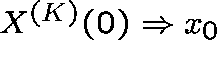 , then,
for all
, then,
for all ![]() and
and ![]() ,
,
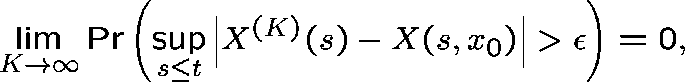
where ![]() is the unique solution to the
above system of differential equations
with
is the unique solution to the
above system of differential equations
with ![]() .
.
So, for example, 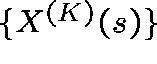 converges in probability
to
converges in probability
to ![]() and, since for each s,
and, since for each s, 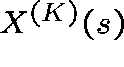 is
uniformly bounded, dominated convergence implies that
is
uniformly bounded, dominated convergence implies that
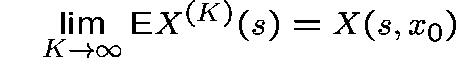
on all finite time intervals.
If 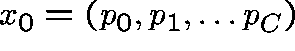 is an equilibrium point it must be of the form given by
is an equilibrium point it must be of the form given by
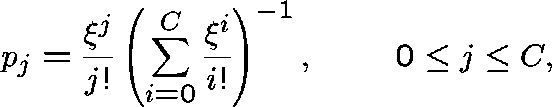
where ![]() solves
solves
![]()
The quantity ![]() , given by
, given by
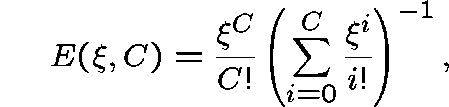
is Erlang's formula for the loss probability of a single
link with C circuits and with Poisson traffic offered at rate ![]() .
It is usually more convenient to calculate the equilibrium points
by setting
.
It is usually more convenient to calculate the equilibrium points
by setting ![]() and solving the equation
and solving the equation
![]()
The central limit law (Theorem 4.2 of [1]) shows that the
random fluctuations about any given equilibrium point, ![]() , are
approximately Gaussian.
Moreover, it shows that these fluctuations can be
approximated by an Ornstein-Uhlenbeck (OU) process.
, are
approximately Gaussian.
Moreover, it shows that these fluctuations can be
approximated by an Ornstein-Uhlenbeck (OU) process.
Let ![]() be an equilibrium point. Then, if
be an equilibrium point. Then, if
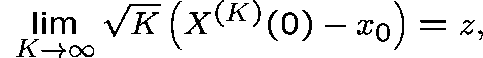
the family of processes 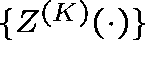 , defined by
, defined by
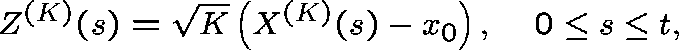
converges weakly to an Ornstein-Uhlenbeck process with initial value Z(0)=z and with a local drift matrix, B, and a local covariance matrix, G, which can be determined from the parameters of the model.
In particular, Z(s) is normally distributed with mean
![]()
and covariance matrix
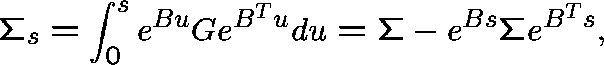
where ![]() , the stationary covariance matrix, satisfies
, the stationary covariance matrix, satisfies
![]()
We can conclude that, for K large, 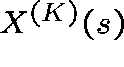 has an approximate normal distribution for each s, and
an approximation for the mean and the covariance matrix of
has an approximate normal distribution for each s, and
an approximation for the mean and the covariance matrix of 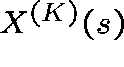 is
given by
is
given by
![]()
and
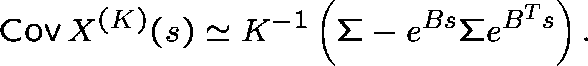
If C=1 (one circuit on each link), set
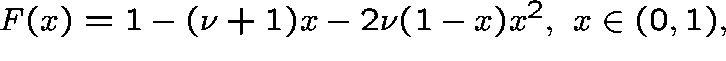
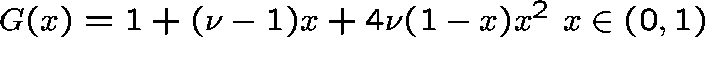 .
Then, F has a unique zero,
.
Then, F has a unique zero, ![]() , on (0,1),
for all
, on (0,1),
for all ![]() (stable equilibrium point of
dx/dt=F(x)).
Further,
(stable equilibrium point of
dx/dt=F(x)).
Further, 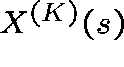 has an approximate
normal distribution with
has an approximate
normal distribution with
![]()
where 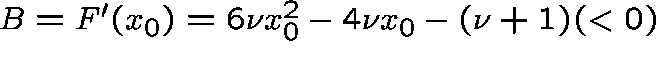 , and
, and
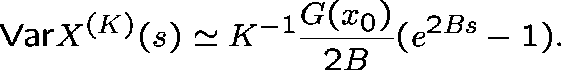
The magnitude of B, and hence the stability of ![]() ,
increases as
,
increases as ![]() becomes large, but the stationary variance,
becomes large, but the stationary variance,
![]() , increases from 0 to a maximum around
, increases from 0 to a maximum around ![]() and then
decreases to 0.
and then
decreases to 0.
When C>1, change coordinates:
![]()
where the rows of A are the left-eigenvectors of ![]() .
Since the column sums of B are all equal to 0, B has a zero eigenvalue, and
so one of the components of
.
Since the column sums of B are all equal to 0, B has a zero eigenvalue, and
so one of the components of ![]() , say
, say 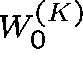 ,
is identically zero, since
because
,
is identically zero, since
because 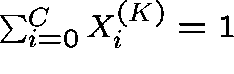 , we have that
, we have that
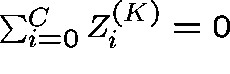 .
.
The sequence 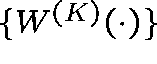 , where (for convenience)
, where (for convenience)
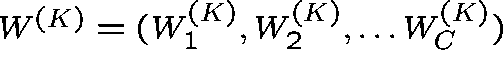 ,
converges weakly to an OU process,
,
converges weakly to an OU process,
![]() , whose individual components are, themselves, OU processes.
Its local drift matrix is
, whose individual components are, themselves, OU processes.
Its local drift matrix is
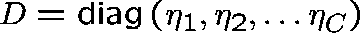 ,
where
,
where ![]() are the non-zero eigenvalues of B,
and its local covariance matrix, S, is obtained from the matrix
are the non-zero eigenvalues of B,
and its local covariance matrix, S, is obtained from the matrix ![]() by deleting the zeroth row and column.
by deleting the zeroth row and column.
In particular, W(s) has a properly C-dimensional normal distribution with
![]() ,
,
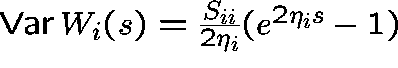
and
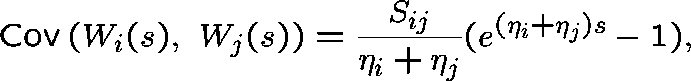
for ![]() , where w=Az.
, where w=Az.
The change of coordinates allows us to use some powerful results
of Andrew Barbour, which establish asymptotic
results on the time of first exit of 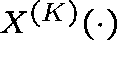 from a region
containing
from a region
containing ![]() .
.
For example, suppose that ![]() is a stable and let
is a stable and let
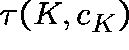 be the time when
be the time when 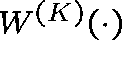 first crosses the contour
first crosses the contour
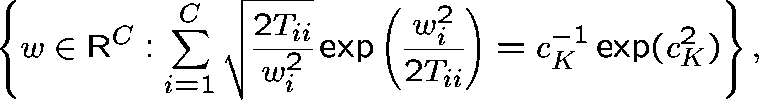
where T, the stationary covariance matrix of ![]() , has
elements
, has
elements ![]() and
and ![]() is
a sequence which tends to
is
a sequence which tends to ![]() ;
to order
;
to order ![]() , the contour delimits the rectangle
, the contour delimits the rectangle
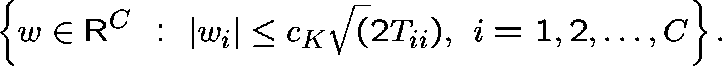
Then, if 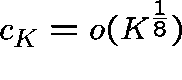 ,
the random variable
,
the random variable
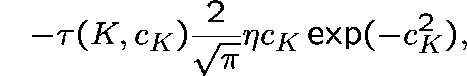
where 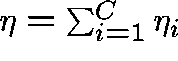 ,
converges weakly to a unit-mean exponential random variable
as
,
converges weakly to a unit-mean exponential random variable
as ![]() .
Thus, provided
.
Thus, provided 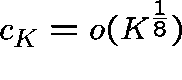 , the
time at which
, the
time at which 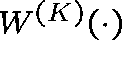 first crosses the contour is of order
first crosses the contour is of order
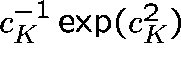 .
.
The corresponding result for the C=1 case is more straightforward.
One can show that
the time that 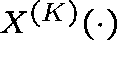 first leaves the interval
first leaves the interval
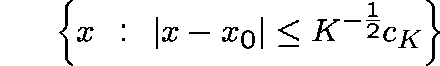
is of order
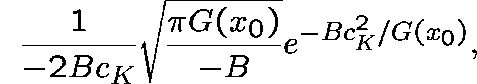
whenever 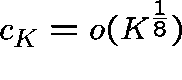 .
Hence, it is asymptotically larger than any power of K if, for example,
.
Hence, it is asymptotically larger than any power of K if, for example,
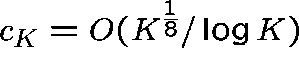 .
.