1c) The first step is to translate the argument into symbolic form. To form an argument we need a collection of premises and a conclusion. The conclusion is normally the statement which begins with "Therefore", "Hence" or "Thus". In this case, there are three premises. The first premise is "If the cat fiddled or the cow jumped over the moon, then the little dog laughed." The second premise is "If the little dog laughed, then the dish ran away with the spoon." The third premise is "But the dish did not run away with the spoon." The conclusion is "Therefore the cat did not fiddle."
Let c represent "the cat fiddled", let j represent "the cow jumped over the moon", let d represent "the little dog laughed", and let r represent "the dish ran away with the spoon." Now write each of the premises and the conclusion in symbolic form.
The first premise (p1) is "If the cat fiddled or the cow
jumped over the moon, then the little dog laughed." This can be written symbolically
as (c V j)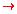 
d.
The second premise (p2) is "If the little dog laughed, then the dish ran
away with the spoon." This can be written symbolically as d
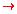r.
The third premise (p3) is "But the dish did not run away with the
spoon." This can be written symbolically as ~r.
The conclusion (q) is "Therefore the cat did not fiddle." This can be written
symbolically as ~c.
Remember that an argument is written as a conjunction of the premises
implies the conclusion. So this argument can be represented as
[(c V j) 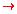d) L (d 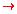r)
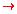L (~r)] (~c).
There are several methods which may be used to determine if this argument is valid. Since the truth table approach will require a truth table with 16 rows, we recommend that you use the other approach but both are included here. If you would like to use a the truth table approach, click here. If you would like to use an approach which tries to determine whether the argument can be invalid, click here.