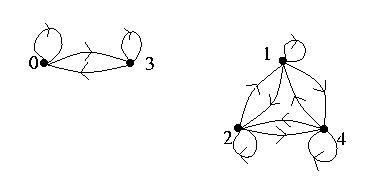
2. a) The directed graph for R is :

b) Since all the vertices have loops, R is
reflexive.
Whenever the edge (u, v) is in the graph, the edge (v, u) is also in the graph, so R is symmetric.
Whenever the edges (u, v) and (v, w) are in the graph, the edge (u, w) is also in the
graph, so R is transitive.
Hence R is an equivalence relation.
c) The graph consists of separate groups of vertices (that is, the vertices occur in groups for which no vertices from different groups are conncected by an edge but all vertices within a group have loops on them and are connected in all possible ways). These groups provide the partition of the set A and hence the equivalence classes of A. In a sense, all the vertices within a group are equivalent since they are related in all possible ways to all the vertices within that group.
The partition of the set A is {0, 3} {1, 2, 4}.
There are two equivalence classes of R: [0] = [3] = {0, 3} and [1] = [2] = [4] = {1, 2, 4}.