Chapter Ten
Relations
Section 10.1
Relations On Sets
The following solutions make use of information found on pages 533 - 543 of the
textbook.
Exercise 10.1.1: Definitions
Fill in the blanks to complete the following sentences.
- Let A and B be any two sets. Recall that A × B = { (a, b) | a
 A and b
A and b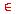 B}.
B}.
- Let A and B be sets. A (binary) relation R from the set
A to the set B is a subset of
A × B.
Given an ordered pair (x, y)
 A × B,
x is related to y by R, if, and only if,
the ordered pair (x, y) is in R.
A × B,
x is related to y by R, if, and only if,
the ordered pair (x, y) is in R.
The expression x is related to y by R can be abreviated as
x R y.
- Arrow diagram of a relation. A relation R from a set A to a set B can
be represented by a directed bipartite graph G. The edge set of G is defined as follows,
for all x
 A and y
A and y B:
B:
$ a directed edge from x to y 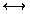 x R y
x R y 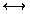 (x, y)
(x, y)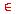 R.
R.
- A function F: A
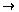 B is a
relation from the set A to the set B that satisfies the following
two properties:
B is a
relation from the set A to the set B that satisfies the following
two properties:
(i) " x  A,
$ y
A,
$ y 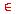 B such that
(x,y)
B such that
(x,y) 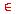 F.
F.
(ii) " x  A and
" y,z
A and
" y,z  B,
if (x,y)
B,
if (x,y) 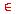 F and
(x,z)
F and
(x,z) 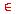 F, then y = z.
F, then y = z.
If F is a function from A to B, we write y = F(x)  (x, y)
(x, y)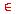 F.
F.
- Let R be a relation from A to B. The inverse relation R-1
from B to A is defined as follows: R-1 = { (y, x)
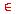 B × A | (x, y)
B × A | (x, y)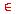 R}.
R}.
- A binary relation on a set A is a binary relation
from A to A.
- If a binary relation R is defined on a set A, then we can represent R using a directed
graph G with vertex set A (no longer a bipartite graph). The edge set of G is defined as
follows: for all x, y
 A,
A,
$ a directed edge from x to y 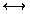 x R y
x R y 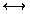 (x, y)
(x, y) 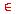 R.
R.
Note that the directed edges are represented as ordered pairs (x, y) and if the element x
is related to itself, then the directed graph G will have a loop
at the vertex x.
Exercise 10.1.2: Examples
You should attempt all these exercises yourself, using the textbook as an aid. Once you
have attempted each question, check your answers by following the appropriate links. If
you are stuck on a question, choose the link that gives you a hint and then try the
question again.
1. Let A = {0, 2, 4} and B = {1, 2, 3, 4}.
a) The Cartesian product A × B consists of the ordered pairs (0, 1), (0, 2), (0, 3), (0, 4), (2, 1), (2, 2), (2, 3), (2, 4), (4, 1), (4, 2), (4, 3),
(4, 4).
b) Now for x A
and y
A
and y B (A and B as above) we say
that x is related to y, x R y, if, and only if, x
B (A and B as above) we say
that x is related to y, x R y, if, and only if, x 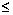 y.
y.
0 R 2 since 0 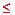 2
2
2 R 4 since 2 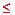 4
4
2 R 3 since 2 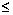 3
3
2 R 2 since 2 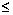 2
2
4 not R 3 since 4 > 3
2. Let A = {1, 2, 3, 4, 5} and B = {0, 2, 4, 6, 8}. Suppose r
is a relation from A to B which is defined as follows. Write down the elements of r.
( i ) x r y 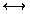 x
x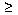 y.
y.
( ii ) x r y 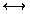 x = y.
x = y.
( iii ) x r y 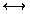 x - y is even.
x - y is even.
( iv ) x r y 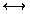 x + y = 7.
x + y = 7.
Hint
Full solution
3. Define three different relations from the set of integers Z to the
set of natural numbers N. (There are many, many answers here, so be
creative.)
Hint
Full solution
4. Consider the following relations on Z:
( i ) R1 = { (a, b) | a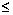 b};
b};
( ii ) R2 = { (a, b) | a > b};
( iii ) R3 = { (a, b) | a = b or a = -b};
( iv ) R4 = { (a, b) | a = b};
( v ) R5 = { (a, b) | a = b+1};
( vi ) R6 = { (a, b) | a + b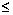 3}.
3}.
Consider each of the following ordered pairs in turn and state to which of the six
relations above the pair belongs: (1,1), (1,2), (2,1), (1,-1) and (2,2).
Full solution
5. Let A = {1, 3, 5} and B = {1, 2, 3, 4}. Draw a directed bipartite graph to
illustrate the relation S from A to B where: (x, y) S
S 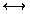 x + 1 > y.
x + 1 > y.
Hint
Full solution
6. Let A = {3, 6, 9} and B = {2, 4, 6, 8}. Let R = { (3,2), (6,2), (9,6), (6,8) } be a
relation. Is R a function from A to B? Explain your answer.
Hint
Full solution
7. Let A = {x, y, z} and B = {1, 4, 7, 10}. Suppose that R = { (x, 4), (x, 10), (z, 1),
(y, 7), (y, 1) } is a relation from A to B. List the elements of R-1.
Full solution
8. Let A = {1, 2, 3, ..., 10} and define a binary relation R on A as follows: " x, y A,
x R y
A,
x R y 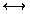 3 | (x - y).
3 | (x - y).
a) Write down the elements of R.
b) Write down the elements of R-1. Is R = R-1?
Hint
Full solution
Section 10.2
Reflexivity, Symmetry and Transitivity
The following solutions make use of information found on pages 546 - 553 of the
textbook.
Exercise 10.2.1: Definitions
Fill in the blanks to complete the following sentences.
- Let R be a binary relation on a set A.
( i ) R is reflexive if, and only if, for all x A, x R x.
A, x R x.
In terms of the directed graph for the relation R, saying that R is reflexive
is equivalent to saying that there is a loop at each vertex
of the graph.
If R is specified as a list of ordered pairs, then R is reflexive if, and
only if, the ordered pair (x, x) is an element of R, for all
x A.
A.
( ii ) R is symmetric if, and only if, for all x, y A, if x R
y then y R x.
A, if x R
y then y R x.
In terms of the directed graph for the relation R, saying that R is symmetric
is equivalent to saying that whenever the directed edge (u, v) is in the graph, then the
directed edge (v, u) is also in the graph.
If R is specified as a list of ordered pairs, then R is symmetric if, and
only if, whenever (x, y) R then the
ordered pair (y, x) also belongs to R.
R then the
ordered pair (y, x) also belongs to R.
( iii ) R is transitive if, and only if, for all x, y, z A, if x R
y and y R z then x R z.
A, if x R
y and y R z then x R z.
In terms of the directed graph for the relation R, saying that R is transitive
is equivalent to saying that whenever the directed edges (u, w) and (w, v) are in the
graph, then the directed edge (u, v) is also in the graph.
If R is specified as a list of ordered pairs, then R is transitive if,
and only if, whenever (x, y) R and
(y, z)
R and
(y, z) R then the ordered pair (x, z) also belongs to R.
R then the ordered pair (x, z) also belongs to R.
- Let R be a binary relation on a set A.
( i ) R is not reflexive if, and only if, there
exists an element a in A such that a is
not related to a by R.
( ii ) R is not symmetric if, and only if, there
exist elements a and b in A such
that a R b but b is not related to a by R.
( iii ) R is not transitive if, and only if, there
exist elements a, b and c in A such
that a R b and b R c but a is not
related to c by R.
- In the directed graph for a relation, if at least one vertex does not have a loop, then
the relation is not reflexive (unless the relation is Ø).
- R is the identity relation on A if, and only if,
"
x, y
 A, x R y
A, x R y 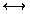 x = y. The identity relation is
also the identity function.
x = y. The identity relation is
also the identity function.
Exercise 10.2.2: Examples
You should attempt all these exercises yourself, using the textbook as an aid. Once you
have attempted each question, check your answers by following the appropriate links. If
you are stuck on a question, choose the link that gives you a hint and then try the
question again.
1. Consider the following relations on the set {1, 2, 3, 4}.
R1 = { (1,1), (1,2), (2,1), (2,2), (3,4), (4,1), (4,4) }
R2 = { (1,1), (1,2), (2,1), (2,2), (3,3), (4,4) }
R3 = { (1,1), (1,2), (1,4), (2,1), (2,2), (3,3), (4,1), (4,4)}
R4 = { (2,1), (3,1), (3,2), (4,1), (4,2), (4,3) }
R5 = { (1,1), (1,2), (1,3), (1,4), (2,2), (2,3), (2,4), (3,3), (3,4), (4,4)}
R6 = { (1,1), (2,2), (3,3), (4,4) }
For each of the relations R1, R2, R3, R4, R5
and R6, determine if the relation is reflexive, symmetric and/or transitive.
Hint
Full solution
2. Is the "divides" relation R, where a R b 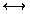 a | b, on the set of positive
integers: i) reflexive? ii) symmetric?
iii) transitive?
a | b, on the set of positive
integers: i) reflexive? ii) symmetric?
iii) transitive?
Hint
Full solution
3. Let A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} and define a relation R on A as
follows: " x, y A, x R y
A, x R y 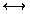 3 | (x - y).
3 | (x - y).
Draw the directed graph of R and use it to check whether R is reflexive, symmetric and/or
transitive. (Note that you have already written out the elements of this relation in
Section 10.1, Question 8 so use that to draw the graph.)
Hint
Full solution
4. Define a relation s on R (the set of all
real numbers) as follows: for all x, y R, x s y
R, x s y 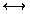 x > y.
x > y.
a) Is s reflexive?
b) Is s symmetric?
c) Is s transitive?
Justify your answers.
Hint
Full solution
5. Define a relation r on Z × (Z
\ {0}) as follows: for all (a, b), (c, d) Z × (Z \ {0}), (a,
b) r (c, d)
Z × (Z \ {0}), (a,
b) r (c, d) 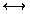 a/b = c/d.
a/b = c/d.
a) Is r reflexive?
b) Is r symmetric?
c) Is r transitive?
Hint
Full solution
6. Prove that if a relation R is reflexive then R-1 is also reflexive.
Hint
Full solution
7. Prove that a relation R is symmetric if and only if R = R-1.
Hint
Full solution
8. For the relation R, is the statement "If R is transitive then R-1 is
transitive'' true or false?
Justify your answer.
Hint
Full solution
Section 10.3
Equivalence Relations
The following solutions make use of information found on pages 555 - 570 of the
textbook.
Exercise 10.3.1: Definitions
Fill in the blanks to complete the following sentences.
- Recall that a partition of a set A is a
collection of nonempty mutually disjoint subsets
of A whose union is A.
- Given a partition {A1, A2, ..., An}
of a set A the binary relation R induced by the partition
is defined on A as follows: for all x, y
 A,
A,
x R y if, and only if x and y are in the
same subset of A within the partition.
- Theorem: Given a partition
{A1, A2, ..., An}
of a set A and a binary relation R induced
by the partition. Then R is
reflexive, symmetric and transitive.
- Let A be a nonempty set and R a binary relation on A.
R is an equivalence
relation if, and only if,
R is reflexive, symmetric and
transitive.
- Let A be a nonempty set and R be an equivalence relation on A.
For each element a in A, the equivalence
class of a, denoted [a]R is the set of
elements x in A such that x is related to a
by R.
Symbolically: [a]R = {x A | x R
a}.
A | x R
a}.
- Let A be a nonempty set and R be an equivalence relation on A. The
distinct equivalence classes of R form a partition of A. Hence A is
equal to the union of the equivalence classes
of R and for any two distinct equivalence classes
[a]R and [b]R,
[a]R
Ç
[b]R =
Æ.
- Let m and n be integers and let d be a positive integer. Recall
the notation m
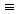 n (mod d)
is read "m is congruent to n modulo d" and is equivalent
to
m - n = kd for some integer k.
n (mod d)
is read "m is congruent to n modulo d" and is equivalent
to
m - n = kd for some integer k.
Hence, m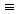 n (mod
d) if, and only if, d
| (m - n).
n (mod
d) if, and only if, d
| (m - n).
The relation R where m R n if, and only if, m is congruent to n
modulo d is an equivalence
relation for all integers m and n and positive integers d.
You will be asked to find the equivalence classes for R later in this section.
Exercise 10.3.2: Examples
You should attempt all these exercises yourself, using the textbook as an aid. Once you
have attempted each question, check your answers by following the appropriate links. If
you are stuck on a question, choose the link that gives you a hint and then try the
question again.
1. Let A = {1, 3, 5, 7, 9, 11, 13} and consider the following partition of A: {1, 5,
9}, {3, 7, 13}, {11}.
List the elements of the relation R induced by this partition.
Hint
Full solution
2. Let A = {0, 1, 2, 3, 4} and define a relation R on A as follows:
R = { (0, 0), (2, 1), (0, 3), (1, 1), (3, 0), (1, 4), (4, 1), (2, 2), (2, 4), (3, 3), (4,
4), (1, 2), (4, 2) }.
a) Draw the directed graph for R.
b) Use the directed graph for R to check whether R is an equivalence relation.
c) If R is an equivalence relation, use the graph to list the partition of the set A
which induces the relation R and to list the equivalence classes of R.
Hint
Full solution
3. Which of the relations in Section 10.2, Question 1 are equivalence relations? For
each relation which is an equivalence relation, draw the directed graph and then use the
graph to list the partition of the set {1, 2, 3, 4} which induces the relation and to list
the equivalence classes for that relation.
Hint
Full solution
4. Define the relation r on the set of integers Z
as follows: for all m and n in Z, m r n 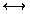 7 | (m - n).
7 | (m - n).
a) Prove that r is an equivalence relation.
b) Find the equivalence classes for r.
c) Refer to the equivalence classes from part b) to determine which of the following
statements are correct? Explain your answers.
( i ) [1] = [-8]; ( ii ) [1] = [8]; ( iii
) [123] = [319]; ( iv ) [304] = [10]; ( v )
[-34] = [-6].
Hint
Full solution
5. Let
A0 = { ..., -10, -5, 0, 5, 10, 15, 20, 25, ...};
A1 = { ..., -9, -4, 1, 6, 11, 16, 21, 26, ...};
A2 = { ..., -8, -3, 2, 7, 12, 17, 22, 27, ...};
A3 = { ..., -7, -2, 3, 8, 13, 18, 23, 28, ...};
A4 = { ..., -6, -1, 4, 9, 14, 19, 24, 29, ...}.
a) Prove that A0, A1, A2, A3 and A4
partition the set of integers Z.
b) Find the relation s induced by this partition.
Hint
Full solution
6. Let d be a positive integer. Define the relation d on the
set of integers Z as follows: for all m and n in Z
m d n 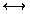 m
m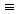 n (mod d). (Recall that m
n (mod d). (Recall that m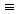 n (mod d) if and only if d |
(m - n).)
n (mod d) if and only if d |
(m - n).)
a) Prove that d is an equivalence relation.
b) List the equivalence classes for d.
Hint
Full solution
Section 10.5
Partial Order Relations
The following solutions make use of information found on pages 585 - 588 and 592 of the
textbook.
Exercise 10.5.1: Definitions
Fill in the blanks to complete the following sentences.
- Let R be a relation on a set A. R is said to be
antisymmetric if, and only if,
" a, b
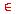 A, if a R b and b R a
then a = b.
A, if a R b and b R a
then a = b.
- In terms of the directed graph for a relation on a set A,
saying that a relation is
antisymmetric is the same as saying that whenever there is a directed edge going from
vertex a to another distinct vertex b, there is
no directed edge
going from vertex b to vertex a.
- Let R be a binary relation defined on a set A. R is said to be
a partial order
relation if, and only if, R is reflexive, antisymmetric and
transitive.
- Let R be a partial order relation on a set A. R is a total order relation
on A if for any two elements a and b in A either a R b
or b R a.
Exercise 10.5.2: Examples
You should attempt all these exercises yourself, using the textbook as an aid. Once you
have attempted each question, check your answers by following the appropriate links. If
you are stuck on a question, choose the link that gives you a hint and then try the
question again.
1. For each of the following relations on the set A = {1, 2, 3, 4}, decide whether it
is antisymmetric. Justify your answers using the directed graph for each relation.
a) R1 = { (1, 1), (2, 2), (2, 3), (2, 4), (4, 4), (3, 3), (3, 4) }
b) R2 = { (1, 2), (2, 3), (3, 4) }
c) R3 = { (1, 3), (1, 4), (2, 3), (2, 4), (3, 1), (3, 4) }
Hint
Full solution
2. Determine whether the relation R on the set of all people is reflexive,
antisymmetric, and/or transitive, where for any two people a and b (a, b) R if and only if :
R if and only if :
a) a is taller than b.
b) a and b were born on the same day.
Hint
Full solution
3. For each of the following relations, determine if the relation is reflexive,
symmetric, antisymmetric and/or transitive. Then classify the relation as a partial order
relation, an equivalence relation or neither.
a) (x, y) R if, and only if,
xy
R if, and only if,
xy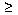 1 where x and y are
integers.
1 where x and y are
integers.
b) (x, y) R if, and only if, x is
a multiple of y where x and y are positive integers.
R if, and only if, x is
a multiple of y where x and y are positive integers.
c) (x, y) R if, and only if, x
R if, and only if, x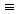 y (mod 13) where x and y are
integers.
y (mod 13) where x and y are
integers.
Hint
Full solution
4. a) List all the 16 relations on the set {0, 1}. Hint: A relation on the set {0, 1}
is a subset of {0, 1}×{0, 1} = { (0, 0), (0, 1), (1, 0), (1, 1) }.
b) Which of the 16 relations on {0, 1}, which you listed in part a), are partial order
relations?
Hint
Full solution
5. Let A = {1, 2, 3, 4} and define the relation r on the
power set of A, P(A), as follows: for X, Y P(A),
P(A),
X r Y 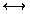 X
Ì Y or X = Y.
X
Ì Y or X = Y.
Show that r is a partial order relation.
Hint
Full solution
6. The partial order relation R is described by the following directed graph.
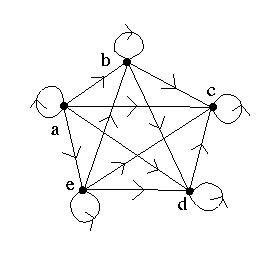
Is R a total order relation on {a, b, c, d, e}? Justify your answer.
Hint
Full solution
7. a) Is the relation r defined in Question 5 a total order
relation on the set A = {1, 2, 3, 4}?
b) What if r were defined in the same way on P(B) where B =
{1}?
Hint
Full solution
Back to workbook solution page
