Solution for Section 10.5 Question 3
3. a) This relation is not reflexive. There
exists an integer, x = 0, for which x is not related to x, since 0·0 is not
greater than or equal to 1.
This relation is symmetric. For all integers x and y,
if x R y, then y R x since if x·y 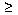 1, then y·x
1, then y·x 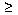 1.
1.
This relation is not antisymmetric. There exist
integers x and y such that x R y and y R x, for example 2·4 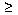 1 and 4·2
1 and 4·2 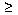 1..
1..
This relation is transitive. For all integers x, y and z, if
x R y and y R z, then x R z.
To prove this, consider the possible values for x, y and z in terms of being negative
integers, positive integers or zero.
None of x, y and z can be 0.
If x, y and z are all positive integers, then x·z 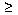 1.
1.
If at least one of x, y or z is negative, then all three of them must be negative, in
which case x·z 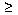 1.
1.
This relation is neither an equivalence
relation nor a partial order relation.
b) This relation is reflexive. For every positive integer
x, x R x since x is a multiple of x.
This relation is not symmetric. There exist positive integers
x and y, x = 6 and y = 2 such that x R y but y is not related to x, that is, 6 is a
multiple of 2, but 2 is not a multiple of 6.
This relation is antisymmetric. For all distinct positive
integers x and y, if x R y then y is not related to x.
If x is a multiple of y, then x = y · k for some integer k ( k is not equal to 1 since
they are distinct positive integers, so k > 1).
Hence y = x · (1/k) and (1/k) is not an
integer for k > 1. Therefore y is not a multiple of x.
This relation is transitive. For all positive integers
x, y and z, if x R y and y R z, then x R z.
If x is a multiple of y and y is a multiple of z, then x = y · k for some
integer k and y = z · h for some integer h. Therefore x = (z · h) · k
= z · d for some integer d. Hence x is a multiple of z.
This relation is a partial order relation.
c) This relation is reflexive. For every integer x, x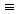 x (mod 13).
x (mod 13).
This relation is symmetric. For all integers x and y, if x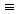 y (mod 13), then y
y (mod 13), then y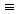 x (mod 13).
x (mod 13).
This relation is not antisymmetric. There exist distinct
integers, x = 1 and y = 14 such that x R y and y R x.
This relation is transitive. For all integers x, y and z, if
x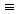 y (mod 13) and y
y (mod 13) and y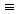 z (mod 13), then x
z (mod 13), then x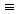 z (mod 13).
z (mod 13).
This relation is an equivalence relation.
Back to Section 10.5