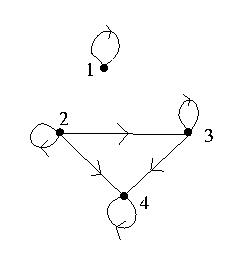
1. a) The directed graph for R1 = { (1, 1), (2, 2), (2, 3), (2, 4), (4, 4), (3, 3), (3, 4) } is:

The relation R1 is antisymmetric since whenever the directed edge (u, v) is in the graph, the directed edge (v, u) is not in the graph.
b) The directed graph for R2 = { (1, 2), (2, 3), (3, 4) } is:
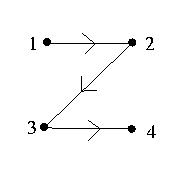
The relation R2 is antisymmetric since whenever the directed edge (u, v) is in the graph, the directed edge (v, u) is not in the graph.
c) The directed graph for R3 = { (1, 3), (1, 4), (2, 3), (2, 4), (3, 1), (3, 4) } is:
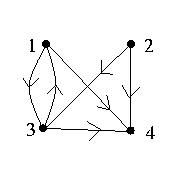
The relation R3 is not antisymmetric since the edges (1, 3) and (3, 1) are both in the graph. Note that although the relation R3 is not antisymmetic, it is also not symmetric.