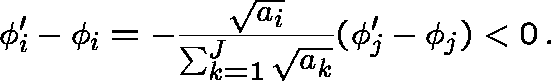
OPTIMAL ALLOCATION OF EFFORT IN GENERAL QUEUEING NETWORKS
by
Phil Pollett
Department of Mathematics
The University of Queensland
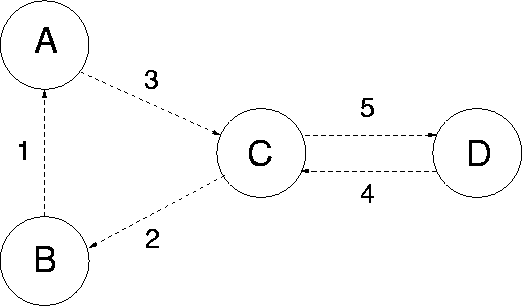
PACKET SWITCHING NETWORKS

A packet switching network with 4 nodes (labelled A,B,C and D) and 5 links (labelled 1,2,...,5)
PACKET SWITCHING NETWORKS
N switching nodes (labelled ![]() )
)
J links (labelled ![]() )
)
Poisson traffic on route ![]() at rate
at rate ![]()
(type-mn traffic)
Common expected message length: ![]() (bits)
(bits)
(Message lengths have an arbitrary distribution which does not depend on type)
Transmission rate on link j is ![]() (bits/sec.)
(bits/sec.)
(There is a first-come first-served (FCFS) discipline at each link)
ROUTING MECHANISMS
Fixed routing
Define R(m,n) to be the collection of (distinct) links used by type-mn traffic:
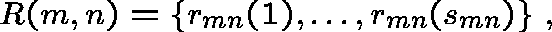
where
is the number of links on route
and
is the link used at stage s.
Random alternative routing
This can be accommodated within the framework of fixed routing by allowing a finer classification of type (mni):
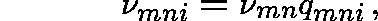
where
is the probability that alternative route i is chosen; there is fixed set of alternative routes for each OD pair (m,n).
PACKET SWITCHING NETWORK AND CORRESPONDING QUEUEING NETWORK

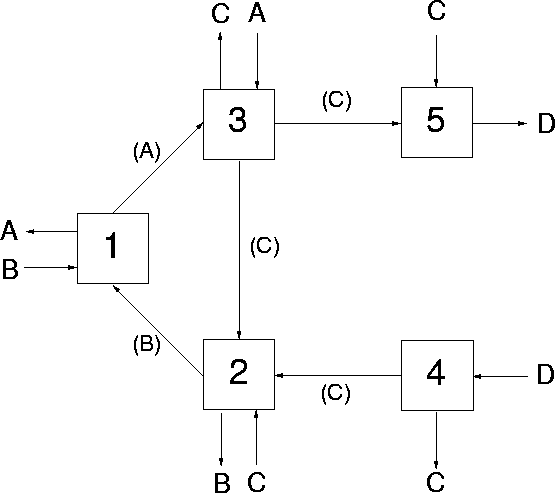
A NETWORK OF QUEUES
Links ![]() queues
queues
Messages ![]() customers
customers
T - set of customer types
![]() - arrival rate of type-t customers
- arrival rate of type-t customers
(Independent Poisson streams)
Route for type-t customers:
![]()
A NETWORK OF QUEUES
If message lengths have an exponential distribution the links behave independently (indeed, as if they were isolated), each with independent streams of Poisson offered traffic (independent among types). For example, if
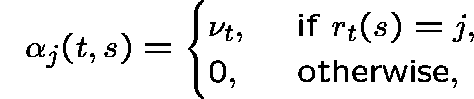
so that the arrival rate at link j is given by
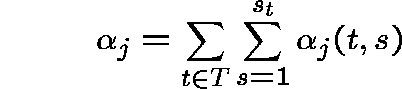
and the demand by ![]() (bits/sec), then,
if the system is stable (
(bits/sec), then,
if the system is stable ( ![]() for each j), the expected
number of messages at link j is
for each j), the expected
number of messages at link j is
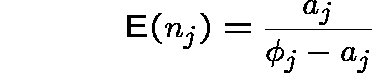
and the expected delay is
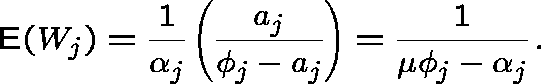
THE INDEPENDENCE ASSUMPTION
Kleinrock (1964) proposed the following assumption: that successive messages requesting transmission along any given link have lengths which are independent and identically distributed, and that message lengths at different links are independent.
Thus, we shall assume that at link j message lengths have a
distribution function ![]() which has mean
which has mean 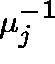 and
variance
and
variance ![]() .
.
Even under this assumption, the model (now a network of ![]() queues with a FCFS discipline) is not analytically tractable.
To make progress, we shall use the Residual-life Approximation
(Pollett (1984)).
queues with a FCFS discipline) is not analytically tractable.
To make progress, we shall use the Residual-life Approximation
(Pollett (1984)).
THE RESIDUAL LIFE APPROXIMATION
Let ![]() be the distribution function of the queueing
time at link j: the time a message spends in the buffer
before transmission. The Residual-Life Approximation
(RLA) provides an accurate approximation for
be the distribution function of the queueing
time at link j: the time a message spends in the buffer
before transmission. The Residual-Life Approximation
(RLA) provides an accurate approximation for ![]() :
:
where
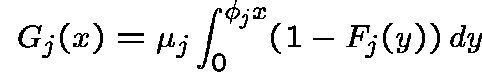
and 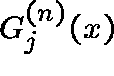 denotes the n-fold convolution of
denotes the n-fold convolution of ![]() . The
distribution of
. The
distribution of ![]() , the number of messages at link j,
used in (2)
is that of the corresponding quasireversible network
of symmetric queues obtained by imposing a symmetry
condition at each link j. In the present context, this
amounts to replacing FCFS by
a last-come first-served (LCFS) discipline.
, the number of messages at link j,
used in (2)
is that of the corresponding quasireversible network
of symmetric queues obtained by imposing a symmetry
condition at each link j. In the present context, this
amounts to replacing FCFS by
a last-come first-served (LCFS) discipline.
THE RESIDUAL LIFE APPROXIMATION
One immediate consequence of (2) is that the expected queueing
time ![]() is approximately
is approximately
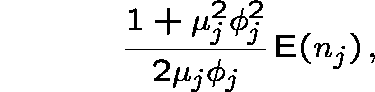
where ![]() is the expected number of messages at link j in the
quasireversible network. Hence, the expected delay at link j is
approximated as follows:
is the expected number of messages at link j in the
quasireversible network. Hence, the expected delay at link j is
approximated as follows:
In the RLA, it is only ![]() which changes
when the service discipline is altered. For the present FCFS discipline
which changes
when the service discipline is altered. For the present FCFS discipline
![]() is given by
is given by
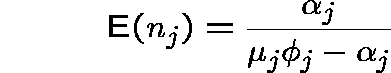
OPTIMAL ALLOCATION OF EFFORT
We shall minimize the average network delay, or equivalently the average number of messages in the network:
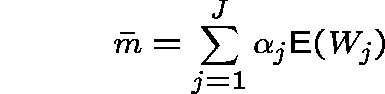
(using the RLA for ![]() ).
).
$F - overall network budget
![]() ($-seconds/bit)
- cost of operating link j
($-seconds/bit)
- cost of operating link j
(The cost of operating link j is proportional to the capacity)
Thus, we should choose the capacities subject to the cost constraint
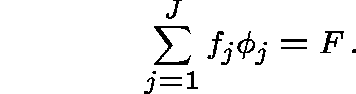
THE PROBLEM
Let 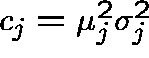 be the squared coefficient of variation of
be the squared coefficient of variation of
![]() and let
and let ![]() .
.
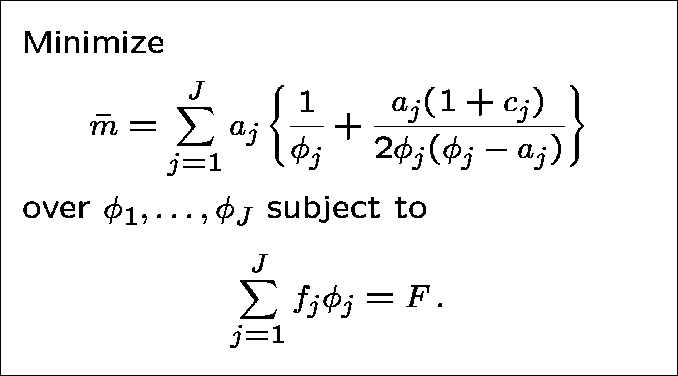
Introduce a lagrange multiplier ![]() ; our
problem then becomes one of minimizing
; our
problem then becomes one of minimizing
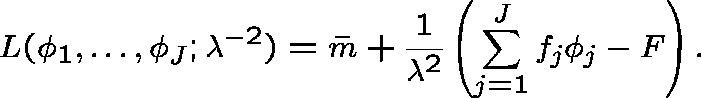
Setting ![]() yields a quartic
polynomial equation in
yields a quartic
polynomial equation in ![]() :
:
where ![]() .
.
Find solutions
such that ![]() (recall that this latter condition is a
requirement for stability).
(recall that this latter condition is a
requirement for stability).
Using the transformation
the problem reduces to one with unit costs ![]() ;
equation (6) becomes
;
equation (6) becomes
and the constraint becomes
EXPONENTIAL SERVICE TIMES
If transmission times are exponentially distributed ( ![]() for
each j) it is easy to verify that (10) has a unique solution on
for
each j) it is easy to verify that (10) has a unique solution on
![]() given by
given by
![]()
Upon application of the constraint (12) we arrive at the optimal capacity assignment
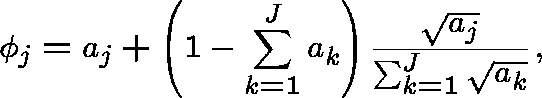
for unit costs. In the case of general costs this becomes
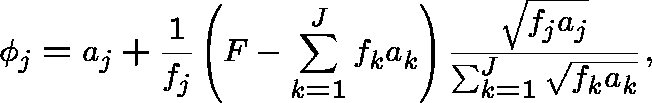
after applying the transformation (8). This is a result obtained by Kleinrock (1964).
THE GENERAL CASE
We shall adopt a perturbation approach, assuming that the lagrange multiplier and the optimal allocation take the following forms:
where by 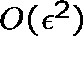 we mean terms of order
we mean terms of order ![]() .
The zero
.
The zero ![]() order terms come from Kleinrock's solution:
order terms come from Kleinrock's solution:
![]()
where
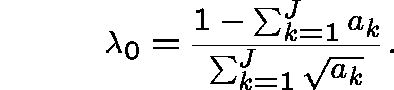
FIRST-ORDER SOLUTION
On substituting (14) into (10) we obtain an expression for
![]() in terms of
in terms of ![]() , which in turn is calculated
using the constraint (12) and by setting
, which in turn is calculated
using the constraint (12) and by setting ![]() (the Kronecker delta).
(the Kronecker delta).
To first order, the optimal allocation is
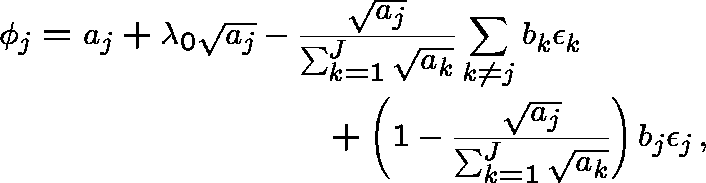
where
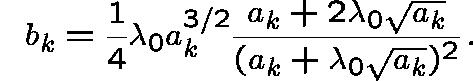
SENSITIVITY
Let ![]() ,
, ![]() , be the new optimal allocation obtained
after incrementing
, be the new optimal allocation obtained
after incrementing ![]() by a small quantity
by a small quantity ![]() . We find
that, to first order in
. We find
that, to first order in ![]() ,
,
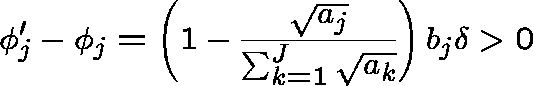
and, for ![]() ,
,