Bottlenecks in Markovian Queueing Networks
by
Phil Pollett

Department of Mathematics
The University of Queensland
Bottlenecks in Markovian Queueing Networks
by
Phil Pollett

Department of Mathematics
The University of Queensland
OUR SETTING
A closed network of queues:
BOTTLENECKS
Common sense:
SIMPLE EXAMPLES
All nodes have infinitely many servers:
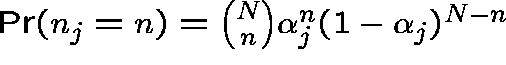 ,
,
![]() , where
, where ![]() (<1) is proportional to the arrival
rate at node j divided by service rate. Clearly
(<1) is proportional to the arrival
rate at node j divided by service rate. Clearly ![]() for
each n as
for
each n as ![]() , and so all nodes are bottlenecks.
, and so all nodes are bottlenecks.
All nodes have a single server:
The distribution of ![]() cannot be written down explicitly, but we can
show that if there is a node j whose traffic intensity is
strictly greater than the others, it is the unique bottleneck.
cannot be written down explicitly, but we can
show that if there is a node j whose traffic intensity is
strictly greater than the others, it is the unique bottleneck.
Moreover, for each node k in the remainder of the network, the
distribution of ![]() approaches a geometric distribution with parameter
approaches a geometric distribution with parameter
![]() in the limit as
in the limit as ![]() , and
, and ![]() , for
, for ![]() , are asymptotically independent.
, are asymptotically independent.
MARKOVIAN NETWORKS
Our only assumption:
The steady-state (joint) distribution ![]() of the numbers of customers
of the numbers of customers
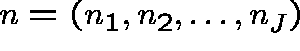 at the various nodes has the product form
at the various nodes has the product form
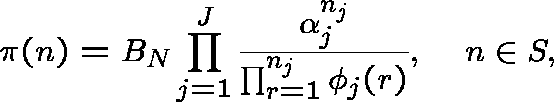
where S is the finite subset of ![]() with
with ![]() and
and ![]() is a normalizing constant chosen so that
is a normalizing constant chosen so that ![]() sums to unity over S.
sums to unity over S.
Here ![]() is proportional to the amount of service
requirement (in items per minute) coming into node j (this will
actually be equal to
is proportional to the amount of service
requirement (in items per minute) coming into node j (this will
actually be equal to ![]() ).
Suppose (wlog) that
).
Suppose (wlog) that ![]() .
.
![]() is the service effort at node j (in items per
minute) when there are n customers present. We shall assume that
is the service effort at node j (in items per
minute) when there are n customers present. We shall assume that
![]() and
and ![]() whenever
whenever ![]() .
.
GENERATING FUNCTIONS
Our primary tool:
Define generating functions ![]() by
by
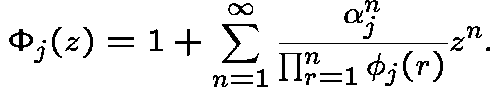
It is easily shown that 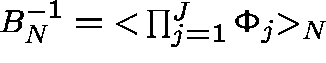 , where
, where
![]() takes the
takes the ![]() coefficient of a power series.
The marginal distribution of
coefficient of a power series.
The marginal distribution of ![]() can be evaluated as
can be evaluated as
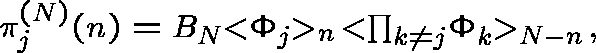
for ![]() .
.
SINGLE-SERVER NODES
Suppose that each node j has a single server ( ![]() for
for ![]() ).
Then,
).
Then, ![]() and so
and so
![]() .
Summing
.
Summing
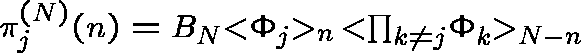
over n, and recalling that 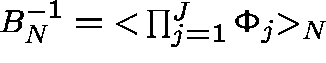 ,
gives
,
gives ![]() .
.
Suppose that ![]() , so that node J has maximal traffic intensity.
, so that node J has maximal traffic intensity.
If we can prove that ![]() as
as ![]() , then
, then
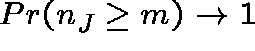 (node J is a bottleneck) and
(node J is a bottleneck) and
![]() for j<J (the others are not).
for j<J (the others are not).
WHY DOES ![]() ?
?
Define ![]() , where now
, where now ![]() .
Clearly
.
Clearly ![]() has radius of convergence (RC)
has radius of convergence (RC) ![]() ; in
particular,
; in
particular, ![]() (
( ![]() ) has RC
) has RC ![]() .
.
Claim:
![]() has RC
has RC ![]() for all i, so that
for all i, so that
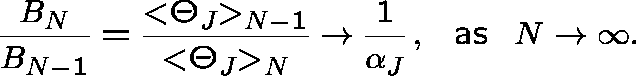
Proof:
Suppose ![]() has RC
has RC ![]() and consider
and consider
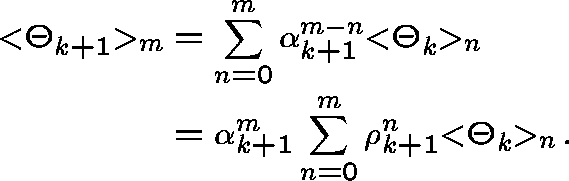
Clearly ![]() , since
, since ![]() , and so
, and so
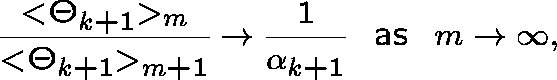
implying that ![]() has RC
has RC ![]() .
.
THE GENERAL CASE
Message: Bottleneck behaviour depends on the relative sizes
of the radii of convergence of the power series
![]() .
.
Proposition 1:
Suppose ![]() has radius of
convergence
has radius of
convergence ![]() and that
and that ![]() . Suppose also that
. Suppose also that
has a limit as ![]() . Then, node J is a bottleneck.
. Then, node J is a bottleneck.
Example:
Suppose node j has ![]() servers, so that the traffic intensity at
node j is proportional to
servers, so that the traffic intensity at
node j is proportional to ![]() . Since
. Since
![]() , we have
, we have ![]() , and so
, and so
![]() . Therefore
. Therefore ![]() is proportional to the reciprocal of the traffic intensity at node j.
It can be shown that (2) holds.
is proportional to the reciprocal of the traffic intensity at node j.
It can be shown that (2) holds.
COMPOUND BOTTLENECKS
What happens when the generating functions corresponding to two or more nodes share the same minimal RC?
Proposition 2:
In the setup of Proposition 1,
suppose that ![]() and that
and that ![]() for
for ![]() .
Then, nodes
.
Then, nodes ![]() behave jointly as a bottleneck in that
behave jointly as a bottleneck in that
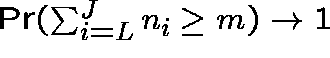 as
as ![]() .
.
It might be conjectured that when the generating functions corresponding
to two nodes share the same minimal RC, they are
always bottlenecks individually. However, while this is true
when all nodes have a single server (because ![]() ), it is not true in general.
), it is not true in general.
SOME EXAMPLES
Consider a network with J=2 nodes and suppose that
![]() . In the following examples
. In the following examples ![]() and
and ![]() have the same RC
have the same RC ![]() .
.
Only one node is a bottleneck:<
Suppose that 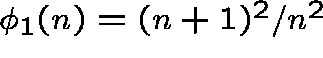 and
and ![]() for
for ![]() .
Then, it can be shown that
.
Then, it can be shown that
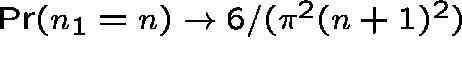 and
and ![]() as
as ![]() .
.
Neither node is a bottleneck:
Suppose that
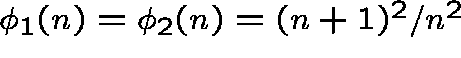 for
for ![]() .
Then,
.
Then,
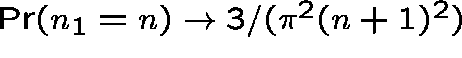 as
as ![]() .
.
AND FINALLY ...
Proposition 4:
Suppose that ![]() have the same
strictly minimal RC
have the same
strictly minimal RC ![]() , and that
, and that ![]() converges
monotonically for some
converges
monotonically for some ![]() . Then, node 1 is a
bottleneck if and only if
. Then, node 1 is a
bottleneck if and only if
![]()
A sufficient condition for node 1 to be a bottleneck is that
![]() diverges at its RC and
diverges at its RC and

This latter condition is not necessary:
In the setup of the previous examples, suppose that
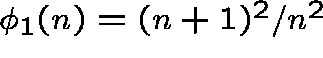 and
and 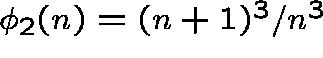 for
for ![]() . Then,
. Then,
![]() and
and ![]() have common RC
have common RC ![]() and both
converge at their RC. But, it can be shown that
and both
converge at their RC. But, it can be shown that ![]() is bounded above by a quantity which is
is bounded above by a quantity which is 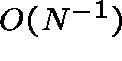 as
as ![]() ,
implying that node 1 is a bottleneck.
,
implying that node 1 is a bottleneck.